Related Research Articles

In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

Calculus is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.

Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.

In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation. Integration started as a method to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Today integration is used in a wide variety of scientific fields.

In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve.

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.

In mathematics, an infinitesimal number is a quantity that is closer to zero than any standard real number, but that is not zero. The word infinitesimal comes from a 17th-century Modern Latin coinage infinitesimus, which originally referred to the "infinity-th" item in a sequence.

Gilles Personne de Roberval, French mathematician, was born at Roberval near Beauvais, France. His name was originally Gilles Personne or Gilles Personier, with Roberval the place of his birth.

La Géométrie was published in 1637 as an appendix to Discours de la méthode, written by René Descartes. In the Discourse, he presents his method for obtaining clarity on any subject. La Géométrie and two other appendices, also by Descartes, La Dioptrique (Optics) and Les Météores (Meteorology), were published with the Discourse to give examples of the kinds of successes he had achieved following his method.

In mathematics, the witch of Agnesi is a cubic plane curve defined from two diametrically opposite points of a circle. It gets its name from Italian mathematician Maria Gaetana Agnesi, and from a mistranslation of an Italian word for a sailing sheet. Before Agnesi, the same curve was studied by Fermat, Grandi, and Newton.
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present day.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.
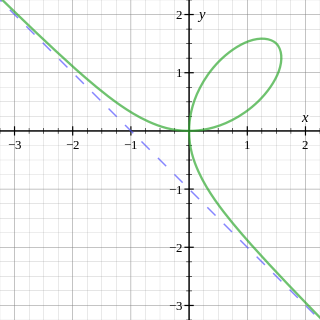
In geometry, the folium of Descartes is an algebraic curve defined by the implicit equation

Pierre de Fermat was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he is recognized for his discovery of an original method of finding the greatest and the smallest ordinates of curved lines, which is analogous to that of differential calculus, then unknown, and his research into number theory. He made notable contributions to analytic geometry, probability, and optics. He is best known for his Fermat's principle for light propagation and his Fermat's Last Theorem in number theory, which he described in a note at the margin of a copy of Diophantus' Arithmetica. He was also a lawyer at the Parlement of Toulouse, France.
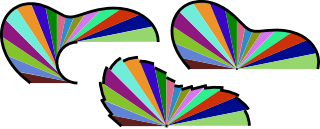
Visual calculus, invented by Mamikon Mnatsakanian, is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner called "aha! solutions" or Roger Nelsen a proof without words.
A timeline of calculus and mathematical analysis.
This is a timeline of pure and applied mathematics history. It is divided here into three stages, corresponding to stages in the development of mathematical notation: a "rhetorical" stage in which calculations are described purely by words, a "syncopated" stage in which quantities and common algebraic operations are beginning to be represented by symbolic abbreviations, and finally a "symbolic" stage, in which comprehensive notational systems for formulas are the norm.

In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:
Adequality is a technique developed by Pierre de Fermat in his treatise Methodus ad disquirendam maximam et minimam to calculate maxima and minima of functions, tangents to curves, area, center of mass, least action, and other problems in calculus. According to André Weil, Fermat "introduces the technical term adaequalitas, adaequare, etc., which he says he has borrowed from Diophantus. As Diophantus V.11 shows, it means an approximate equality, and this is indeed how Fermat explains the word in one of his later writings.". Diophantus coined the word παρισότης (parisotēs) to refer to an approximate equality. Claude Gaspard Bachet de Méziriac translated Diophantus's Greek word into Latin as adaequalitas. Paul Tannery's French translation of Fermat’s Latin treatises on maxima and minima used the words adéquation and adégaler.
References
- Katz, V. (2008), A History of Mathematics:An Introduction, Addison Wesley
- Range, R. Michael (May 2011), "Where Are Limits Needed in Calculus?", American Mathematical Monthly, 118 (5): 404–417, doi:10.4169/amer.math.monthly.118.05.404