Midpoint-stretching polygon

Last updated
A cyclic polygon (green), its midpoint polygon (red), and its midpoint-stretching polygon (pink) Midpoint stretching polygon.svg
A cyclic polygon (green), its midpoint polygon (red), and its midpoint-stretching polygon (pink)

In geometry, the midpoint-stretching polygon of a cyclic polygon P is another cyclic polygon inscribed in the same circle, the polygon whose vertices are the midpoints of the circular arcs between the vertices of P. [1] It may be derived from the midpoint polygon of P (the polygon whose vertices are the edge midpoints) by placing the polygon in such a way that the circle's center coincides with the origin, and stretching or normalizing the vector representing each vertex of the midpoint polygon to make it have unit length.

Geometry Branch of mathematics that studies the shape, size and position of objects

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

In geometry, a vertex is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.

Midpoint middle point of a line segment

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

Contents

Musical application

The midpoint-stretching polygon is also called the shadow of P; when the circle is used to describe a repetitive time sequence and the polygon vertices on it represent the onsets of a drum beat, the shadow represents the set of times when the drummer's hands are highest, and has greater rhythmic evenness than the original rhythm. [2]

Drum beat rhythmic pattern played on drums

A drum beat or drum pattern is a rhythmic pattern, or repeated rhythm establishing the meter and groove through the pulse and subdivision, played on drum kits and other percussion instruments. As such a "beat" consists of multiple drum strokes occurring over multiple musical beats while the term "drum beat" may also refer to a single drum stroke which may occupy more or less time than the current pulse. Many drum beats define or are characteristic of specific music genres.

Maximal evenness

In scale (music) theory a maximally even set (scale) is one in which every generic interval has either one or two consecutive integers specific interval sizes—in other words a scale whose notes (pcs) are "spread out as much as possible." This property was first described by John Clough and Jack Douthett. Clough and Douthett also introduced the maximally even algorithm. For a chromatic cardinality c, a pcset D of cardinality d is maximally enen if and only if there exists an integer m, 0 ≤ m ≤ c - 1 such that

Convergence to regularity

The midpoint-stretching polygon of a regular polygon is itself regular, and iterating the midpoint-stretching operation on an arbitrary initial polygon results in a sequence of polygons whose shape converges to that of a regular polygon. [1] [3]

In Euclidean geometry, a regular polygon is a polygon that is equiangular and equilateral. Regular polygons may be either convex or star. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

Related Research Articles

In elementary geometry, a polygon is a plane figure that is described by a finite number of straight line segments connected to form a closed polygonal chain or polygonal circuit. The solid plane region, the bounding circuit, or the two together, may be called a polygon.

Hexagon shape with six sides

In geometry, a hexagon is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

Cyclic quadrilateral Quadrilateral whose vertices can all fall on a single circle

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

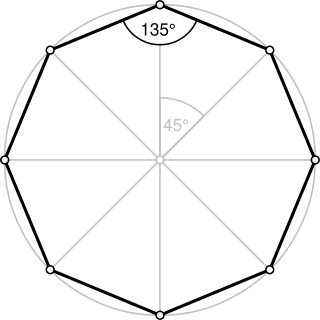
Octagon shape with eight sides

In geometry, an octagon. Is an eight-sided polygon or 8-gon.

Concyclic points a set of points that lie on a single circle

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.

In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

Rectification (geometry) process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points

In Euclidean geometry, rectification or complete-truncation is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

lines in a plane or higher-dimensional space are said to be concurrent if they intersect at a single point.

Inscribed figure

In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about figure F". A circle or ellipse inscribed in a convex polygon is tangent to every side or face of the outer figure. A polygon inscribed in a circle, ellipse, or polygon has each vertex on the outer figure; if the outer figure is a polygon or polyhedron, there must be a vertex of the inscribed polygon or polyhedron on each side of the outer figure. An inscribed figure is not necessarily unique in orientation; this can easily be seen, for example, when the given outer figure is a circle, in which case a rotation of an inscribed figure gives another inscribed figure that is congruent to the original one.

Centre (geometry) middle of the object in geometry

In geometry, a center of an object is a point in some sense in the middle of the object. According to the specific definition of center taken into consideration, an object might have no center If geometry is regarded as the study of isometry groups then a center is a fixed point of all the isometries which move the object onto itself.

Rotating calipers

In computational geometry, the method of rotating calipers is an algorithm design technique that can be used to solve optimization problems including finding the width or diameter of a set of points.

In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.

Pentagon shape with five sides

In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.

Inscribed square problem unsolved problem in geometry of whether every simple closed curve in the plane contains four points at the corners of a square

The inscribed square problem, also known as the square peg problem or the Toeplitz' conjecture, is an unsolved question in geometry: Does every plane simple closed curve contain all four vertices of some square? This is true if the curve is convex or piecewise smooth and in other special cases. The problem was proposed by Otto Toeplitz in 1911. Some early positive results were obtained by Arnold Emch and Lev Schnirelmann. As of 2017, the general case remains open.

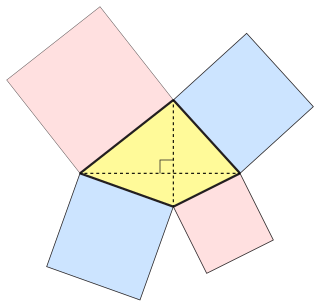
Orthodiagonal quadrilateral quadrilateral in which the diagonals cross at right angles

In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.

Midpoint polygon polygon whose vertices are the midpoints of the edges of another polygon

In geometry, the midpoint polygon of a polygon P is the polygon whose vertices are the midpoints of the edges of P. It is sometimes called the Kasner polygon after Edward Kasner, who termed it the inscribed polygon "for brevity".

Tangential polygon convex polygon that contains an inscribed circle

In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle. This is a circle that is tangent to each of the polygon's sides. The dual polygon of a tangential polygon is a cyclic polygon, which has a circumscribed circle passing through each of its vertices.

References

  1. 1 2 Ding, Jiu; Hitt, L. Richard; Zhang, Xin-Min (1 July 2003), "Markov chains and dynamic geometry of polygons" (PDF), Linear Algebra and Its Applications, 367: 255–270, doi:10.1016/S0024-3795(02)00634-1 , retrieved 19 October 2011.
  2. ↑ Gomez-Martin, Francisco; Taslakian, Perouz; Toussaint, Godfried T. (2008), "Evenness preserving operations on musical rhythms", Proceedings of the 2008 C3S2E conference (PDF), doi:10.1145/1370256.1370275 .
  3. ↑ Gomez-Martin, Francisco; Taslakian, Perouz; Toussaint, Godfried T. (2008), "Convergence of the shadow sequence of inscribed polygons", 18th Fall Workshop on Computational Geometry
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.