The beam diameter or beam width of an electromagnetic beam is the diameter along any specified line that is perpendicular to the beam axis and intersects it. Since beams typically do not have sharp edges, the diameter can be defined in many different ways. Five definitions of the beam width are in common use: D4σ, 10/90 or 20/80 knife-edge, 1/e2, FWHM, and D86. The beam width can be measured in units of length at a particular plane perpendicular to the beam axis, but it can also refer to the angular width, which is the angle subtended by the beam at the source. The angular width is also called the beam divergence.
In electromagnetics, especially in optics, beam divergence is an angular measure of the increase in beam diameter or radius with distance from the optical aperture or antenna aperture from which the beam emerges. The term is relevant only in the "far field", away from any focus of the beam. Practically speaking, however, the far field can commence physically close to the radiating aperture, depending on aperture diameter and the operating wavelength.

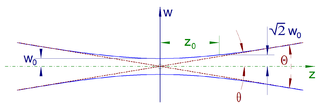
In optics, a Gaussian beam is a beam of monochromatic electromagnetic radiation whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of most (but not all) lasers, as such a beam can be focused into the most concentrated spot. When such a beam is refocused by a lens, the transverse phase dependence is altered; this results in a different Gaussian beam. The electric and magnetic field amplitude profiles along any such circular Gaussian beam (for a given wavelength and polarization) are determined by a single parameter: the so-called waist w0. At any position z relative to the waist (focus) along a beam having a specified w0, the field amplitudes and phases are thereby determined as detailed below.

In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another, provided there is no refractive power at the interface. The exact definition of the term varies slightly between different areas of optics. Numerical aperture is commonly used in microscopy to describe the acceptance cone of an objective, and in fiber optics, in which it describes the range of angles within which light that is incident on the fiber will be transmitted along it.
Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.
Optical tweezers are scientific instruments that use a highly focused laser beam to hold and move microscopic and sub-microscopic objects like atoms, nanoparticles and droplets, in a manner similar to tweezers. If the object is held in air or vacuum without additional support, it can be called optical levitation.

In optics, the Airy disk and Airy pattern are descriptions of the best-focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light. The Airy disk is of importance in physics, optics, and astronomy.
A transverse mode of electromagnetic radiation is a particular electromagnetic field pattern of the radiation in the plane perpendicular to the radiation's propagation direction. Transverse modes occur in radio waves and microwaves confined to a waveguide, and also in light waves in an optical fiber and in a laser's optical resonator.

An optical cavity, resonating cavity or optical resonator is an arrangement of mirrors that forms a standing wave cavity resonator for light waves. Optical cavities are a major component of lasers, surrounding the gain medium and providing feedback of the laser light. They are also used in optical parametric oscillators and some interferometers. Light confined in the cavity reflects multiple times, producing standing waves for certain resonance frequencies. The standing wave patterns produced are called modes; longitudinal modes differ only in frequency while transverse modes differ for different frequencies and have different intensity patterns across the cross-section of the beam.
The Kerr effect, also called the quadratic electro-optic (QEO) effect, is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change is directly proportional to the square of the electric field instead of varying linearly with it. All materials show a Kerr effect, but certain liquids display it more strongly than others. The Kerr effect was discovered in 1875 by John Kerr, a Scottish physicist.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the object is given by the Fresnel diffraction equation.

The Fresnel number (F), named after the physicist Augustin-Jean Fresnel, is a dimensionless number occurring in optics, in particular in scalar diffraction theory.
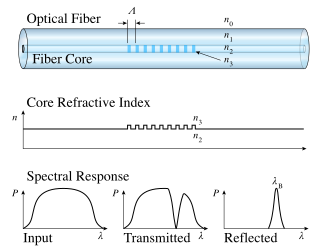
A fiber Bragg grating (FBG) is a type of distributed Bragg reflector constructed in a short segment of optical fiber that reflects particular wavelengths of light and transmits all others. This is achieved by creating a periodic variation in the refractive index of the fiber core, which generates a wavelength-specific dielectric mirror.Hence a fiber Bragg grating can be used as an inline optical fiber to block certain wavelengths or it can be used as wavelength-specific reflector.

An optical vortex is a zero of an optical field; a point of zero intensity. The term is also used to describe a beam of light that has such a zero in it. The study of these phenomena is known as singular optics.
In laser science, the beam parameter product (BPP) is the product of a laser beam's divergence angle (half-angle) and the radius of the beam at its narrowest point. The BPP quantifies the quality of a laser beam, and how well it can be focused to a small spot.
In laser science, the parameter M2, also known as the beam propagation ratio or beam quality factor is a measure of laser beam quality. It represents the degree of variation of a beam from an ideal Gaussian beam. It is calculated from the ratio of the beam parameter product (BPP) of the beam to that of a Gaussian beam with the same wavelength. It relates the beam divergence of a laser beam to the minimum focussed spot size that can be achieved. For a single mode TEM00 (Gaussian) laser beam, M2 is exactly one. Unlike the beam parameter product, M2 is unitless and does not vary with wavelength.

In optics and especially laser science, the Rayleigh length or Rayleigh range, , is the distance along the propagation direction of a beam from the waist to the place where the area of the cross section is doubled. A related parameter is the confocal parameter, b, which is twice the Rayleigh length. The Rayleigh length is particularly important when beams are modeled as Gaussian beams.

A laser beam profiler captures, displays, and records the spatial intensity profile of a laser beam at a particular plane transverse to the beam propagation path. Since there are many types of lasers — ultraviolet, visible, infrared, continuous wave, pulsed, high-power, low-power — there is an assortment of instrumentation for measuring laser beam profiles. No single laser beam profiler can handle every power level, pulse duration, repetition rate, wavelength, and beam size.
In laser science, laser beam quality defines aspects of the beam illumination pattern and the merits of a particular laser beam's propagation and transformation properties. By observing and recording the beam pattern, for example, one can infer the spatial mode properties of the beam and whether or not the beam is being clipped by an obstruction; By focusing the laser beam with a lens and measuring the minimum spot size, the number of times diffraction limit or focusing quality can be computed.
The orbital angular momentum of light (OAM) is the component of angular momentum of a light beam that is dependent on the field spatial distribution, and not on the polarization. It can be further split into an internal and an external OAM. The internal OAM is an origin-independent angular momentum of a light beam that can be associated with a helical or twisted wavefront. The external OAM is the origin-dependent angular momentum that can be obtained as cross product of the light beam position and its total linear momentum.













