Moisture advection is the horizontal transport of water vapor by the wind. Measurement and knowledge of atmospheric water vapor, or "moisture", is crucial in the prediction of all weather elements, especially clouds, fog, temperature, humidity thermal comfort indices and precipitation. Regions of moisture advection are often co-located with regions of warm advection. [1]
Using the classical definition of advection, moisture advection is defined as:
in which V is the horizontal wind vector, and is the density of water vapor. However, water vapor content is usually measured in terms of mixing ratio (mass fraction) in reanalyses or dew point (temperature to partial vapor pressure saturation, i.e. relative humidity to 100%) in operational forecasting. The advection of dew point itself can be thought as moisture advection:
In terms of mixing ratio, horizontal transport/advection can be represented in terms of moisture flux:
in which q is the mixing ratio. The value can be integrated throughout the atmosphere to total transport of moisture through the vertical:
where is the density of air, and P is pressure at the ground surface. For the far right definition, we have used Hydrostatic equilibrium approximation.
And its divergence (convergence) imply net evapotranspiration (precipitation) as adding (removing) moisture from the column:
where P, E, and the integral term are—precipitation, evapotranspiration, and time rate of change of precipitable water, all represented in terms of mass/(unit area * unit time). One can convert to more typical units in length such as mm by multiplying the density of liquid water and the correct length unit conversion factor.
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century.
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of mass, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all.
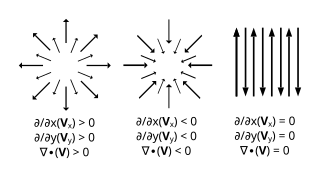
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
In physics, the Navier–Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , , or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf(p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f(p).
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.
In 1851, George Gabriel Stokes derived an expression, now known as Stokes law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. Stokes' law is derived by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a Functional to a change in a function on which the functional depends.
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero.
Stokes flow, also named creeping flow or creeping motion, is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. . This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature this type of flow occurs in the swimming of microorganisms, sperm and the flow of lava. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.
Open-channel flow, a branch of hydraulics and fluid mechanics, is a type of liquid flow within a conduit or in channel with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways but differ in one important respect: the free surface. Open-channel flow has a free surface, whereas pipe flow does not.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
The convection–diffusion equation is a combination of the diffusion and convection (advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation.
The Clausius–Duhem inequality is a way of expressing the second law of thermodynamics that is used in continuum mechanics. This inequality is particularly useful in determining whether the constitutive relation of a material is thermodynamically allowable.
The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system, that is, a measure of the system's overall polarity. The SI units for electric dipole moment are coulomb-meter (C⋅m); however, a commonly used unit in atomic physics and chemistry is the debye (D).
Multipole radiation is a theoretical framework for the description of electromagnetic or gravitational radiation from time-dependent distributions of distant sources. These tools are applied to physical phenomena which occur at a variety of length scales - from gravitational waves due to galaxy collisions to gamma radiation resulting from nuclear decay. Multipole radiation is analyzed using similar multipole expansion techniques that describe fields from static sources, however there are important differences in the details of the analysis because multipole radiation fields behave quite differently from static fields. This article is primarily concerned with electromagnetic multipole radiation, although the treatment of gravitational waves is similar.
In physics, the first law of thermodynamics is an expression of the conservation of total energy of a system. The increase of the energy of a system is equal to the sum of work done on the system and the heat added to that system:
The streamline upwind Petrov–Galerkin pressure-stabilizing Petrov–Galerkin formulation for incompressible Navier–Stokes equations can be used for finite element computations of high Reynolds number incompressible flow using equal order of finite element space by introducing additional stabilization terms in the Navier–Stokes Galerkin formulation.
 | This climatology/meteorology–related article is a stub. You can help Wikipedia by expanding it. |
