Natural process variation

Last updated April 27, 2019

Natural process variation, sometimes just called process variation, is the statistical description of natural fluctuations in process outputs.

Statistics is a branch of mathematics dealing with data collection, organization, analysis, interpretation and presentation. In applying statistics to, for example, a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model process to be studied. Populations can be diverse topics such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments. See glossary of probability and statistics.

Equations

The following equations are used for an x-bar-control chart:

Control charts, also known as Shewhart charts or process-behavior charts, are a statistical process control tool used to determine if a manufacturing or business process is in a state of control.

{\bar {x}}=\sum _{i=1}^{n}x_{i}/n

\sigma _{\bar {x}}=\sigma /{\sqrt {n}}

In the example, with n = 10 samples, the targeted mean, ${\bar {x}}$ , and standard error of the mean, $\sigma _{\bar {x}}$ are:

There are several kinds of means in various branches of mathematics.

{\bar {x}}=1

\sigma _{\bar {x}}=0.1/{\sqrt {1}}0=0.0316

That is, independent 10-sample means should themselves have a standard deviation of 0.0316. It is natural that the means vary this much, for by the central limit theorem the means should have a normal distribution, regardless of the distribution of the samples themselves.

In statistics, the standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of data values. A low standard deviation indicates that the data points tend to be close to the mean of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values.

In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.

In probability theory, the normaldistribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.

The importance of knowing the natural process variation becomes clear when we apply statistical process control. In a stable process, the mean is on target; in the example, the target is the filling, set to 1 litre. The variation within the upper and lower control limits (UCL and LCL) is considered the natural variation of the process.

Statistical process control (SPC) is a method of quality control which employs statistical methods to monitor and control a process. This helps to ensure that the process operates efficiently, producing more specification-conforming products with less waste. SPC can be applied to any process where the "conforming product" output can be measured. Key tools used in SPC include run charts, control charts, a focus on continuous improvement, and the design of experiments. An example of a process where SPC is applied is manufacturing lines.

Usage

When a sample average (size n = 10 in this case) is located outside the control limits, then this is an indication that the process is out of (statistical) control. To be more specific:

The Western Electric rules conclude that the process is out of control if:

One point plots outside the 3σ-limits (the UCL and LCL).
Two out of three consecutive points plot beyond a 2σ-limit.
Four out of five consecutive points plot at a distance of 1σ or beyond from the centerline.
Eight consecutive points plot on one side of the center line.

Goal

The most important goal of understanding the principle of natural process variation is to consider the natural variance in the output before we make any changes to the process. Since SPC tends to minimize the process variations in time, as we better understand the process and have more experience with running it, we try to reduce the variation of it. The knowledge of the principle of natural variance helps us avoid making any unnecessary changes to the process, which might add variance to the process, instead of removing it.

In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its mean. Informally, it measures how far a set of (random) numbers are spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by $,, or .$

Related Research Articles

The weighted arithmetic mean is similar to an ordinary arithmetic mean, except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics.

In probability and statistics, Student's t-distribution is any member of a family of continuous probability distributions that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown. It was developed by William Sealy Gosset under the pseudonym Student.

The power of a binary hypothesis test is the probability that the test rejects the null hypothesis (H₀) when a specific alternative hypothesis (H₁) is true. The statistical power ranges from 0 to 1, and as statistical power increases, the probability of making a type II error (wrongly accepting the null) decreases. For a type II error probability of β, the corresponding statistical power is 1 − β. For example, if experiment 1 has a statistical power of 0.7, and experiment 2 has a statistical power of 0.95, then there is a stronger probability that experiment 1 had a type II error than experiment 2, and experiment 2 is more reliable than experiment 1 due to the reduction in probability of a type II error. It can be equivalently thought of as the probability of accepting the alternative hypothesis (H₁) when it is true—that is, the ability of a test to detect a specific effect, if that specific effect actually exists. That is,

In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given random-sample-based statistic. If an arbitrarily large number of samples, each involving multiple observations, were separately used in order to compute one value of a statistic for each sample, then the sampling distribution is the probability distribution of the values that the statistic takes on. In many contexts, only one sample is observed, but the sampling distribution can be found theoretically.

The t-test is any statistical hypothesis test in which the test statistic follows a Student's t-distribution under the null hypothesis.

The standard error (SE) of a statistic is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM).

A tolerance interval is a statistical interval within which, with some confidence level, a specified proportion of a sampled population falls. "More specifically, a 100×p%/100×(1−α) tolerance interval provides limits within which at least a certain proportion (p) of the population falls with a given level of confidence (1−α)." "A tolerance interval (TI) based on a sample is constructed so that it would include at least a proportion p of the sampled population with confidence 1−α; such a TI is usually referred to as p-content − (1−α) coverage TI." "A upper tolerance limit (TL) is simply a 1−α upper confidence limit for the 100 p percentile of the population."

In probability theory and statistics, the coefficient of variation (CV), also known as relative standard deviation (RSD), is a standardized measure of dispersion of a probability distribution or frequency distribution. It is often expressed as a percentage, and is defined as the ratio of the standard deviation $to the mean . The CV or RSD is widely used in analytical chemistry to express the precision and repeatability of an assay. It is also commonly used in fields such as engineering or physics when doing quality assurance studies and ANOVA gauge R&R. In addition, CV is utilized by economists and investors in economic models and in determining the volatility of a security.$

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by the two parameters, a and b, which are its minimum and maximum values. The distribution is often abbreviated U(a,b). It is the maximum entropy probability distribution for a random variable X under no constraint other than that it is contained in the distribution's support.

Sample size determination is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample. In practice, the sample size used in a study is determined based on the expense of data collection, and the need to have sufficient statistical power. In complicated studies there may be several different sample sizes involved in the study: for example, in a stratified survey there would be different sample sizes for each stratum. In a census, data are collected on the entire population, hence the sample size is equal to the population size. In experimental design, where a study may be divided into different treatment groups, this may be different sample sizes for each group.

In process improvement efforts, the process capability index or process capability ratio is a statistical measure of process capability: the ability of a process to produce output within specification limits. The concept of process capability only holds meaning for processes that are in a state of statistical control. Process capability indices measure how much "natural variation" a process experiences relative to its specification limits and allows different processes to be compared with respect to how well an organization controls them.

In statistics, a pivotal quantity or pivot is a function of observations and unobservable parameters such that the function's probability distribution does not depend on the unknown parameters. A pivot quantity need not be a statistic—the function and its value can depend on the parameters of the model, but its distribution must not. If it is a statistic, then it is known as an ancillary statistic.

Bootstrapping (statistics) statistical method

In statistics, bootstrapping is any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.

In statistics and in particular statistical theory, unbiased estimation of a standard deviation is the calculation from a statistical sample of an estimated value of the standard deviation of a population of values, in such a way that the expected value of the calculation equals the true value. Except in some important situations, outlined later, the task has little relevance to applications of statistics since its need is avoided by standard procedures, such as the use of significance tests and confidence intervals, or by using Bayesian analysis.

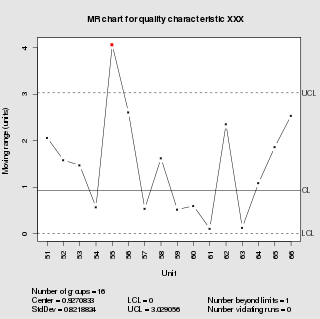
In statistical quality control, the individual/moving-range chart is a type of control chart used to monitor variables data from a business or industrial process for which it is impractical to use rational subgroups.

In probability and statistics, the Tweedie distributions are a family of probability distributions which include the purely continuous normal and gamma distributions, the purely discrete scaled Poisson distribution, and the class of mixed compound Poisson–gamma distributions which have positive mass at zero, but are otherwise continuous. For any random variable Y that obeys a Tweedie distribution, the variance var(Y) relates to the mean E(Y) by the power law,

In statistics, a generalized p-value is an extended version of the classical p-value, which except in a limited number of applications, provides only approximate solutions.

References

Douglas C. Montgomery, George C. Runger. Applied Statistics and Probability for Engineers, 4/e. Wiley, 2006. ISBN 978-0-471-74589-1.
An Introduction to Understanding Variation
Respecting Natural Variation

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.