In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs.
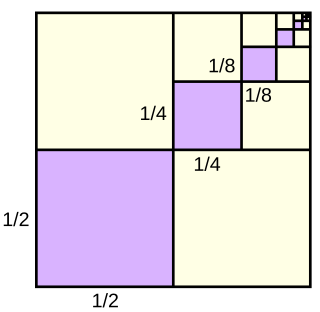
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series
In mathematics, the tensor product of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In mathematics, particularly in linear algebra, a skew-symmetricmatrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is , while an example of a 3×3 diagonal matrix is. An identity matrix of any size, or any multiple of it is a diagonal matrix called scalar matrix, for example, . In geometry, a diagonal matrix may be used as a scaling matrix, since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale.
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or anti-Hermitian if its conjugate transpose is the negative of the original matrix. That is, the matrix is skew-Hermitian if it satisfies the relation
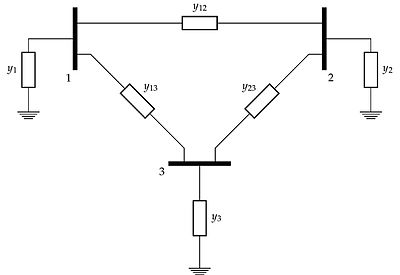
In power engineering, the power-flow study, or load-flow study, is a numerical analysis of the flow of electric power in an interconnected system. A power-flow study usually uses simplified notations such as a one-line diagram and per-unit system, and focuses on various aspects of AC power parameters, such as voltages, voltage angles, real power and reactive power. It analyzes the power systems in normal steady-state operation.
In the mathematical field of graph theory, the Laplacian matrix, also called the graph Laplacian, admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. Named after Pierre-Simon Laplace, the graph Laplacian matrix can be viewed as a matrix form of the negative discrete Laplace operator on a graph approximating the negative continuous Laplacian obtained by the finite difference method.
In mathematics, a symmetric bilinear form on a vector space is a bilinear map from two copies of the vector space to the field of scalars such that the order of the two vectors does not affect the value of the map. In other words, it is a bilinear function that maps every pair of elements of the vector space to the underlying field such that for every and in . They are also referred to more briefly as just symmetric forms when "bilinear" is understood.
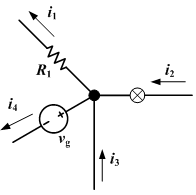
In electric circuits analysis, nodal analysis, node-voltage analysis, or the branch current method is a method of determining the voltage between "nodes" in an electrical circuit in terms of the branch currents.
A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0, 1)-matrix is a matrix with entries from the Boolean domain B = {0, 1}. Such a matrix can be used to represent a binary relation between a pair of finite sets. It is an important tool in combinatorial mathematics and theoretical computer science.
In wireless communications, channel state information (CSI) is the known channel properties of a communication link. This information describes how a signal propagates from the transmitter to the receiver and represents the combined effect of, for example, scattering, fading, and power decay with distance. The method is called channel estimation. The CSI makes it possible to adapt transmissions to current channel conditions, which is crucial for achieving reliable communication with high data rates in multiantenna systems.
Precoding is a generalization of beamforming to support multi-stream transmission in multi-antenna wireless communications. In conventional single-stream beamforming, the same signal is emitted from each of the transmit antennas with appropriate weighting such that the signal power is maximized at the receiver output. When the receiver has multiple antennas, single-stream beamforming cannot simultaneously maximize the signal level at all of the receive antennas. In order to maximize the throughput in multiple receive antenna systems, multi-stream transmission is generally required.
Zero-forcing precoding is a method of spatial signal processing by which a multiple antenna transmitter can null the multiuser interference in a multi-user MIMO wireless communication system. When the channel state information is perfectly known at the transmitter, the zero-forcing precoder is given by the pseudo-inverse of the channel matrix. Zero-forcing has been used in LTE mobile networks.
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) is a multi-criteria decision analysis method, which was originally developed by Ching-Lai Hwang and Yoon in 1981 with further developments by Yoon in 1987, and Hwang, Lai and Liu in 1993. TOPSIS is based on the concept that the chosen alternative should have the shortest geometric distance from the positive ideal solution (PIS) and the longest geometric distance from the negative ideal solution (NIS). A dedicated book in the fuzzy context was published in 2021
In mathematics, the Zassenhaus algorithm is a method to calculate a basis for the intersection and sum of two subspaces of a vector space. It is named after Hans Zassenhaus, but no publication of this algorithm by him is known. It is used in computer algebra systems.
In power engineering, Kron reduction is a method used to reduce or eliminate the desired node without need of repeating the steps like in Gaussian elimination.
Reciprocity in electrical networks is a property of a circuit that relates voltages and currents at two points. The reciprocity theorem states that the current at one point in a circuit due to a voltage at a second point is the same as the current at the second point due to the same voltage at the first. The reciprocity theorem is valid for almost all passive networks. The reciprocity theorem is a feature of a more general principle of reciprocity in electromagnetism.