The nodal period (or draconic period) of a satellite is the time interval between successive passages of the satellite through either of its orbital nodes, [1] [2] typically the ascending node. This type of orbital period applies to artificial satellites, like those that monitor weather on Earth, and natural satellites like the Moon.
It is distinct from the sidereal period, which measures the period with respect to reference stars seemingly fixed onto a spherical background, since the location of a satellite's nodes precess over time. [3] For example, the nodal period of the Moon is 27.2122 days [4] (one draconic month), while its sidereal period is 27.3217 days [5] (one sidereal month).
The oblate figure of the Earth has important effects of the orbits of near-Earth satellites. [6] An expression for the nodal period (Tn) of a near circular orbit, such that the eccentricity (ε) is almost but not equal to zero, is the following: [7]
where is the semi-major axis, is the gravitational constant, is a perturbation factor due to the oblateness of the earth, is the inclination, is the radius of the earth and is the argument of the perigee.
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
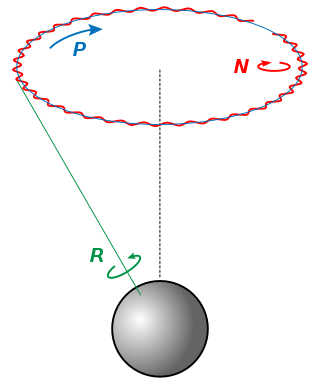
Nutation is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behaviour of a mechanism. In an appropriate reference frame it can be defined as a change in the second Euler angle. If it is not caused by forces external to the body, it is called free nutation or Euler nutation. A pure nutation is a movement of a rotational axis such that the first Euler angle is constant. Therefore it can be seen that the circular red arrow in the diagram indicates the combined effects of precession and nutation, while nutation in the absence of precession would only change the tilt from vertical. However, in spacecraft dynamics, precession is sometimes referred to as nutation.
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the change per unit length, but it is otherwise dimensionless. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.
The wave impedance of an electromagnetic wave is the ratio of the transverse components of the electric and magnetic fields. For a transverse-electric-magnetic (TEM) plane wave traveling through a homogeneous medium, the wave impedance is everywhere equal to the intrinsic impedance of the medium. In particular, for a plane wave travelling through empty space, the wave impedance is equal to the impedance of free space. The symbol Z is used to represent it and it is expressed in units of ohms. The symbol η (eta) may be used instead of Z for wave impedance to avoid confusion with electrical impedance.
The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.
Chebyshev filters are analog or digital filters that have a steeper roll-off than Butterworth filters, and have either passband ripple or stopband ripple. Chebyshev filters have the property that they minimize the error between the idealized and the actual filter characteristic over the range of the filter, but with ripples in the passband. This type of filter is named after Pafnuty Chebyshev because its mathematical characteristics are derived from Chebyshev polynomials. Type I Chebyshev filters are usually referred to as "Chebyshev filters", while type II filters are usually called "inverse Chebyshev filters".
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.
A Sun-synchronous orbit (SSO), also called a heliosynchronous orbit, is a nearly polar orbit around a planet, in which the satellite passes over any given point of the planet's surface at the same local mean solar time. More technically, it is an orbit arranged so that it precesses through one complete revolution each year, so it always maintains the same relationship with the Sun.
Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.
The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:
Orbit determination is the estimation of orbits of objects such as moons, planets, and spacecraft. One major application is to allow tracking newly observed asteroids and verify that they have not been previously discovered. The basic methods were discovered in the 17th century and have been continuously refined.
A ground track or ground trace is the path on the surface of a planet directly below an aircraft's or satellite's trajectory. In the case of satellites, it is also known as a suborbital track, and is the vertical projection of the satellite's orbit onto the surface of the Earth.
In general relativity, Lense–Thirring precession or the Lense–Thirring effect is a relativistic correction to the precession of a gyroscope near a large rotating mass such as the Earth. It is a gravitomagnetic frame-dragging effect. It is a prediction of general relativity consisting of secular precessions of the longitude of the ascending node and the argument of pericenter of a test particle freely orbiting a central spinning mass endowed with angular momentum .
Acoustic streaming is a steady flow in a fluid driven by the absorption of high amplitude acoustic oscillations. This phenomenon can be observed near sound emitters, or in the standing waves within a Kundt's tube. Acoustic streaming was explained first by Lord Rayleigh in 1884. It is the less-known opposite of sound generation by a flow.
Nodal precession is the precession of the orbital plane of a satellite around the rotational axis of an astronomical body such as Earth. This precession is due to the non-spherical nature of a rotating body, which creates a non-uniform gravitational field. The following discussion relates to low Earth orbit of artificial satellites, which have no measurable effect on the motion of Earth. The nodal precession of more massive, natural satellites like the Moon is more complex.
The non-radiative dielectric (NRD) waveguide was introduced by Yoneyama in 1981. In Fig. 1 the crosses shown: it consists of a dielectric rectangular slab of height (a) and width (b), which is placed between two metallic parallel plates of a suitable width. The structure is practically the same as the H waveguide, proposed by Tischer in 1953. Due to the dielectric slab, the electromagnetic field is confined in the vicinity of the dielectric region, whereas in the outside region for suitable frequencies, the electromagnetic field decays exponentially. Therefore, if the metallic plates are sufficiently extended, the field is practically negligible at the end of the plates and therefore the situation does not greatly differ from the ideal case in which the plates are infinitely extended. The polarization of the electric field in the required mode is mainly parallel to the conductive walls. As it is known, if the electric field is parallel to the walls, the conduction losses decrease in the metallic walls at the increasing frequency, whereas, if the field is perpendicular to the walls, losses increase at the increasing frequency. Since the NRD waveguide has been devised for its implementation at millimeter waves, the selected polarization minimizes the ohmic losses in the metallic walls.
This article is about the Bowring series of the transverse mercator. In 1989 Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
In orbital mechanics, a frozen orbit is an orbit for an artificial satellite in which natural drifting due to the central body's shape has been minimized by careful selection of the orbital parameters. Typically, this is an orbit in which, over a long period of time, the satellite's altitude remains constant at the same point in each orbit. Changes in the inclination, position of the apsis of the orbit, and eccentricity have been minimized by choosing initial values so that their perturbations cancel out., which results in a long-term stable orbit that minimizes the use of station-keeping propellant.
