Norman Margolus

Last updated
Norman H. Margolus
Born1955 (age 68–69)
Other namesNorm Margolus
CitizenshipCanadian, American
Alma materMIT
Known for Margolus neighborhood
Margolus gate
Margolus–Levitin theorem
Block cellular automaton
Reversible cellular automaton
CAM-6 accelerator
Computronium
Critters
Scientific career
FieldsComputer Science, Cellular Automata
Website people.csail.mit.edu/nhm/

Norman H. Margolus (born 1955) [1] is a Canadian-American [2] physicist and computer scientist, known for his work on cellular automata and reversible computing. [3] He is a research affiliate with the Computer Science and Artificial Intelligence Laboratory at the Massachusetts Institute of Technology. [4]

Contents

Education and career

Margolus received his Ph.D. in physics in 1987 from the Massachusetts Institute of Technology (MIT) under the supervision of Edward Fredkin. [5] He founded and was chief scientist for Permabit, an information storage device company. [6]

Research contributions

Margolus was one of the organizers of a seminal research meeting on the connections between physics and computation theory, held on Mosquito Island in 1982. [7] He is known for inventing the block cellular automaton and the Margolus neighborhood for block cellular automata, which he used to develop cellular automaton simulations of billiard-ball computers. [3] [8] [9]

In the same work, Margolus also showed that the billiard ball model could be simulated by a second-order cellular automaton, a different type of cellular automaton invented by his thesis advisor, Edward Fredkin. These two simulations were among the first cellular automata that were both reversible (able to be run backwards as well as forwards for any number of time steps, without ambiguity) and universal (able to simulate the operations of any computer program); [10] this combination of properties is important in low-energy computing, as it has been shown that the energy dissipation of computing devices may be made arbitrarily small if and only if they are reversible. [11]

In connection with this issue, Margolus and his co-author Lev B. Levitin proved the Margolus–Levitin theorem showing that the speed of any computer is limited by the fundamental laws of physics to be at most proportional to its energy use; this implies that ultra-low-energy computers must run more slowly than conventional computers. [3] [12] [13]

With Tommaso Toffoli, Margolus developed the CAM-6 cellular automaton simulation hardware, which he extensively described in his book with Toffoli, Cellular Automata Machines (MIT Press, 1987), [3] [14] and with Tom Knight he developed the "Flattop" integrated circuit implementation of billiard-ball computation. [15] He has also done pioneering research on the reversible quantum gate logic needed to support quantum computers. [16]

See also

Related Research Articles

<span class="mw-page-title-main">Cellular automaton</span> Discrete model studied in computer science

A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.

In logic circuits, the Toffoli gate, also known as the CCNOT gate (“controlled-controlled-not”), invented by Tommaso Toffoli, is a CNOT gate with two control qubits and one target qubit. That is, the target qubit will be inverted if the first and second qubits are both 1. It is a universal reversible logic gate, which means that any classical reversible circuit can be constructed from Toffoli gates. Formally, we describe the Toffoli gate with the following truth table and matrix:

Digital physics is a speculative idea that the universe can be conceived of as a vast, digital computation device, or as the output of a deterministic or probabilistic computer program. The hypothesis that the universe is a digital computer was proposed by Konrad Zuse in his 1969 book Rechnender Raum ("Calculating-space"). The term digital physics was coined in 1978 by Edward Fredkin, who later came to prefer the term digital philosophy. Fredkin encouraged the creation of a digital physics group at what was then MIT's Laboratory for Computer Science, with Tommaso Toffoli and Norman Margolus as primary figures.

<span class="mw-page-title-main">Edward Fredkin</span> American physicist and computer scientist (1934–2023)

Edward Fredkin was an American computer scientist, physicist and businessman who was an early pioneer of digital physics.

A cellular automaton (CA) is Life-like if it meets the following criteria:

<span class="mw-page-title-main">Garden of Eden (cellular automaton)</span> Pattern that has no predecessors

In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.

Reversible computing is any model of computation where the computational process, to some extent, is time-reversible. In a model of computation that uses deterministic transitions from one state of the abstract machine to another, a necessary condition for reversibility is that the relation of the mapping from states to their successors must be one-to-one. Reversible computing is a form of unconventional computing.

Tommaso Toffoli is an Italian-American professor of electrical and computer engineering at Boston University where he joined the faculty in 1995. He has worked on cellular automata and the theory of artificial life, and is known for the invention of the Toffoli gate.

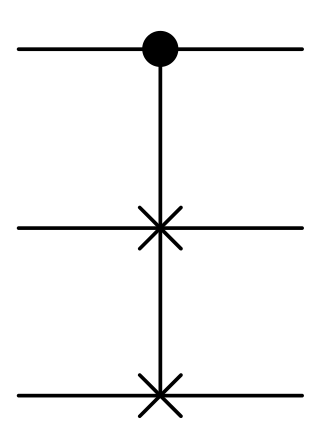
<span class="mw-page-title-main">Fredkin gate</span> Universal reversible logic gate, applied in quantum computing

The Fredkin gate is a computational circuit suitable for reversible computing, invented by Edward Fredkin. It is universal, which means that any logical or arithmetic operation can be constructed entirely of Fredkin gates. The Fredkin gate is a circuit or device with three inputs and three outputs that transmits the first bit unchanged and swaps the last two bits if, and only if, the first bit is 1.

Bremermann's limit, named after Hans-Joachim Bremermann, is a limit on the maximum rate of computation that can be achieved in a self-contained system in the material universe. It is derived from Einstein's mass-energy equivalency and the Heisenberg uncertainty principle, and is c2/h ≈ 1.3563925 × 1050 bits per second per kilogram.

<span class="mw-page-title-main">Second-order cellular automaton</span> Type of reversible cellular automaton

A second-order cellular automaton is a type of reversible cellular automaton (CA) invented by Edward Fredkin where the state of a cell at time t depends not only on its neighborhood at time t − 1, but also on its state at time t − 2.

<span class="mw-page-title-main">Block cellular automaton</span> Kind of cellular automaton

A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.

The limits of computation are governed by a number of different factors. In particular, there are several physical and practical limits to the amount of computation or data storage that can be performed with a given amount of mass, volume, or energy.

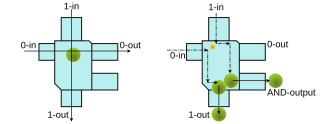
<span class="mw-page-title-main">Billiard-ball computer</span> Type of conservative logic circuit

A billiard-ball computer, a type of conservative logic circuit, is an idealized model of a reversible mechanical computer based on Newtonian dynamics, proposed in 1982 by Edward Fredkin and Tommaso Toffoli. Instead of using electronic signals like a conventional computer, it relies on the motion of spherical billiard balls in a friction-free environment made of buffers against which the balls bounce perfectly. It was devised to investigate the relation between computation and reversible processes in physics.

Humans have considered and tried to create non-biological life for at least 3,000 years. As seen in tales ranging from Pygmalion to Frankenstein, humanity has long been intrigued by the concept of artificial life.

A quantum cellular automaton (QCA) is an abstract model of quantum computation, devised in analogy to conventional models of cellular automata introduced by John von Neumann. The same name may also refer to quantum dot cellular automata, which are a proposed physical implementation of "classical" cellular automata by exploiting quantum mechanical phenomena. QCA have attracted a lot of attention as a result of its extremely small feature size and its ultra-low power consumption, making it one candidate for replacing CMOS technology.

Richard Erwin Cleve is a Canadian professor of computer science at the David R. Cheriton School of Computer Science at the University of Waterloo, where he holds the Institute for Quantum Computing Chair in quantum computing, and an associate member of the Perimeter Institute for Theoretical Physics.

<span class="mw-page-title-main">Reversible cellular automaton</span> Cellular automaton that can be run backwards

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.

<span class="mw-page-title-main">Critters (cellular automaton)</span>

Critters is a reversible block cellular automaton with similar dynamics to Conway's Game of Life, first described by Tommaso Toffoli and Norman Margolus in 1987.

In quantum mechanics, a quantum speed limit (QSL) is a limitation on the minimum time for a quantum system to evolve between two distinguishable (orthogonal) states. QSL theorems are closely related to time-energy uncertainty relations. In 1945, Leonid Mandelstam and Igor Tamm derived a time-energy uncertainty relation that bounds the speed of evolution in terms of the energy dispersion. Over half a century later, Norman Margolus and Lev Levitin showed that the speed of evolution cannot exceed the mean energy, a result known as the Margolus–Levitin theorem. Realistic physical systems in contact with an environment are known as open quantum systems and their evolution is also subject to QSL. Quite remarkably it was shown that environmental effects, such as non-Markovian dynamics can speed up quantum processes, which was verified in a cavity QED experiment.

References

  1. ↑ Birth year as given in the index of Wolfram, Stephen (2002), A New Kind of Science , Wolfram Media, ISBN   1-57955-008-8 .
  2. ↑ He is described as Canadian in Wright, Robert (April 1988), "Did the Universe Just Happen?", The Atlantic Monthly .
  3. 1 2 3 4 Brown, Julian (2002), Minds, Machines, and the Multiuniverse: The Quest for the Quantum Computer, Simon and Schuster, pp. 74–76, ISBN   978-0-7432-4263-9 .
  4. ↑ CSAIL directory Archived 2011-04-26 at the Wayback Machine , accessed 2011-02-03.
  5. ↑ Margolus, Norman H. (1987), Physics and Computation (PDF), Ph.D. thesis, Massachusetts Institute of Technology.
  6. ↑ Shread, Paul (October 27, 2003), "Permabit Makes a Case for CAS", Enterprise IT Planet.
  7. ↑ Regis, Ed (1988), Who Got Einstein's Office?: Eccentricity and Genius at the Institute for Advanced Study , Basic Books, p.  239, ISBN   978-0-201-12278-7 .
  8. ↑ Margolus, N. (1984), "Physics-like models of computation", Physica D, 10 (1–2): 81–95, Bibcode:1984PhyD...10...81M, doi:10.1016/0167-2789(84)90252-5 . Reprinted in Wolfram, Stephen, ed. (1986), Theory and Applications of Cellular Automata, Advanced series on complex systems, vol. 1, World Scientific, pp. 232–246, Bibcode:1986taca.book.....W .
  9. ↑ Schiff, Joel L. (2008), "4.2.1 Partitioning Cellular Automata", Cellular Automata: A Discrete View of the World, Wiley, pp. 115–116.
  10. ↑ Fredkin, Edward, "Chapter 9: History", Introduction to Digital Philosophy (draft), archived from the original on 2012-04-15. A different mechanism for defining reversible universal cellular automata, by embedding d-dimensional irreversible automata into (d + 1)-dimensional reversible automata, was described earlier by Toffoli, Tommaso (1977), "Computation and construction universality of reversible cellular automata" (PDF), Journal of Computer and System Sciences, 15 (2): 213–231, doi: 10.1016/s0022-0000(77)80007-x .
  11. ↑ De Vos, Alexis (2010), Reversible Computing: Fundamentals, Quantum Computing, and Applications, Wiley, ISBN   978-3-527-40992-1 .
  12. ↑ Margolus, Norman; Levitin, Lev B. (1998), "The maximum speed of dynamical evolution", Physica D, 120 (1–2): 188–195, arXiv: quant-ph/9710043 , Bibcode:1998PhyD..120..188M, doi:10.1016/S0167-2789(98)00054-2, S2CID   468290 .
  13. ↑ Lloyd, Seth; Ng, Y. Jack (November 2004), "Black Hole Computers", Scientific American , 291 (5): 53–61, Bibcode:2004SciAm.291e..52L, doi:10.1038/scientificamerican1104-52, PMID   15521147 .
  14. ↑ Ilachinski, Andrew (2001), "A.1.1 CAM-6", Cellular automata: a discrete universe, World Scientific, pp. 713–714, ISBN   978-981-238-183-5 .
  15. ↑ Johnson, George (June 15, 1999), "A Radical Computer Learns to Think in Reverse", New York Times .
  16. ↑ Barenco, Adriano; Bennett, Charles H.; Cleve, Richard; DiVincenzo, David P.; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A.; Weinfurter, Harald (1995), "Elementary gates for quantum computation", Physical Review A, 52 (5): 3457–3467, arXiv: quant-ph/9503016 , Bibcode:1995PhRvA..52.3457B, doi:10.1103/PhysRevA.52.3457, PMID   9912645, S2CID   8764584 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.