The weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of gravitational singularities arising in general relativity.

General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations.

A gravitational singularity, spacetime singularity or simply singularity is a condition in which gravity is predicted to be so intense that spacetime itself would break down catastrophically. As such, a singularity is by definition no longer part of the regular spacetime and cannot be determined by "where" or "when". Gravitational singularities exist at a junction between general relativity and quantum mechanics; therefore, the properties of the singularity cannot be described without an established theory of quantum gravity. Trying to find a complete and precise definition of singularities in the theory of general relativity, the current best theory of gravity, remains a difficult problem. A singularity in general relativity can be defined by the scalar invariant curvature becoming infinite or, better, by a geodesic being incomplete.
In general relativity, Eddington–Finkelstein coordinates are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics. Null geodesics are the worldlines of photons; radial ones are those that are moving directly towards or away from the central mass. They are named for Arthur Stanley Eddington and David Finkelstein. Although they appear to have inspired the idea, neither ever wrote down these coordinates or the metric in these coordinates. Roger Penrose seems to have been the first to write down the null form but credits it to the above paper by Finkelstein, and, in his Adams Prize essay later that year, to Eddington and Finkelstein. Most influentially, Misner, Thorne and Wheeler, in their book Gravitation, refer to the null coordinates by that name.
The Penrose–Hawking singularity theorems are a set of results in general relativity that attempt to answer the question of when gravitation produces singularities. The Penrose singularity theorem is a theorem in semi-Riemannian geometry and its general relativistic interpretation predicts a gravitational singularity in black hole formation. The Hawking singularity theorem is based on the Penrose theorem and it is interpreted as a gravitational singularity in the Big Bang situation. Penrose was awarded the Nobel Prize in Physics in 2020 "for the discovery that black hole formation is a robust prediction of the general theory of relativity", which he shared with Reinhard Genzel and Andrea Ghez.
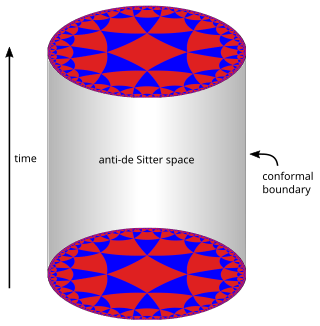
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.

In theoretical physics, a Penrose diagram is a two-dimensional diagram capturing the causal relations between different points in spacetime through a conformal treatment of infinity. It is an extension of the Minkowski diagram of special relativity where the vertical dimension represents time, and the horizontal dimension represents a space dimension. Using this design, all light rays take a 45° path . Locally, the metric on a Penrose diagram is conformally equivalent to the metric of the spacetime depicted. The conformal factor is chosen such that the entire infinite spacetime is transformed into a Penrose diagram of finite size, with infinity on the boundary of the diagram. For spherically symmetric spacetimes, every point in the Penrose diagram corresponds to a 2-dimensional sphere .
Rindler coordinates are a coordinate system used in the context of special relativity to describe the hyperbolic acceleration of a uniformly accelerating reference frame in flat spacetime. In relativistic physics the coordinates of a hyperbolically accelerated reference frame constitute an important and useful coordinate chart representing part of flat Minkowski spacetime. In special relativity, a uniformly accelerating particle undergoes hyperbolic motion, for which a uniformly accelerating frame of reference in which it is at rest can be chosen as its proper reference frame. The phenomena in this hyperbolically accelerated frame can be compared to effects arising in a homogeneous gravitational field. For general overview of accelerations in flat spacetime, see Acceleration and Proper reference frame.
In general relativity, the pp-wave spacetimes, or pp-waves for short, are an important family of exact solutions of Einstein's field equation. The term pp stands for plane-fronted waves with parallel propagation, and was introduced in 1962 by Jürgen Ehlers and Wolfgang Kundt.
An asymptotically flat spacetime is a Lorentzian manifold in which, roughly speaking, the curvature vanishes at large distances from some region, so that at large distances, the geometry becomes indistinguishable from that of Minkowski spacetime.
In physics, a Killing horizon is a geometrical construct used in general relativity and its generalizations to delineate spacetime boundaries without reference to the dynamic Einstein field equations. Mathematically a Killing horizon is a null hypersurface defined by the vanishing of the norm of a Killing vector field. It can also be defined as a null hypersurface generated by a Killing vector, which in turn is null at that surface.
In differential geometry and theoretical physics, the Petrov classification describes the possible algebraic symmetries of the Weyl tensor at each event in a Lorentzian manifold.
In theoretical physics, Nordström's theory of gravitation was a predecessor of general relativity. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström, in 1912 and 1913 respectively. The first was quickly dismissed, but the second became the first known example of a metric theory of gravitation, in which the effects of gravitation are treated entirely in terms of the geometry of a curved spacetime.
In theoretical physics, particularly fringe physics, polarizable vacuum (PV) and its associated theory refer to proposals by Harold Puthoff, Robert H. Dicke, and others to develop an analog of general relativity to describe gravity and its relationship to electromagnetism.
The concept of mass in general relativity (GR) is more subtle to define than the concept of mass in special relativity. In fact, general relativity does not offer a single definition of the term mass, but offers several different definitions that are applicable under different circumstances. Under some circumstances, the mass of a system in general relativity may not even be defined.

The causal sets program is an approach to quantum gravity. Its founding principles are that spacetime is fundamentally discrete and that spacetime events are related by a partial order. This partial order has the physical meaning of the causality relations between spacetime events.
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.
In gravitational theory, the Bondi–Metzner–Sachs (BMS) group, or the Bondi–van der Burg–Metzner–Sachs group, is an asymptotic symmetry group of asymptotically flat, Lorentzian spacetimes at null infinity. It was originally formulated in 1962 by Hermann Bondi, M. G. van der Burg, A. W. Metzner and Rainer K. Sachs in order to investigate the flow of energy at infinity due to propagating gravitational waves. Half a century later, this work of Bondi, van der Burg, Metzner, and Sachs is considered pioneering and seminal. In his autobiography, Bondi considered the 1962 work as his "best scientific work".























