| Order-4-3 pentagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {5,4,3} |
| Coxeter diagram |      |
| Cells | {5,4}  |
| Faces | {5} |
| Vertex figure | {4,3} |
| Dual | {3,4,5} |
| Coxeter group | [5,4,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-3 pentagonal honeycomb or 5,4,3 honeycomb is a regular space-filling tessellation (or honeycomb). Each infinite cell is an order-4 pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-4-3 pentagonal honeycomb is {5,4,3}, with three order-4 pentagonal tilings meeting at each edge. The vertex figure of this honeycomb is a cube, {4,3}.
 Poincaré disk model (Vertex centered) |  Ideal surface |
It is a part of a series of regular polytopes and honeycombs with {p,4,3} Schläfli symbol, and tetrahedral vertex figures:
| Order-4-3 hexagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {6,4,3} |
| Coxeter diagram |  |
| Cells | {6,4}  |
| Faces | {6} |
| Vertex figure | {4,3} |
| Dual | {3,4,6} |
| Coxeter group | [6,4,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-3 hexagonal honeycomb or 6,4,3 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-4 hexagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-4-3 hexagonal honeycomb is {6,4,3}, with three order-4 hexagonal tilings meeting at each edge. The vertex figure of this honeycomb is a cube, {4,3}.
 Poincaré disk model (Vertex centered) |  Ideal surface |
| Order-4-3 heptagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {7,4,3} |
| Coxeter diagram |  |
| Cells | {7,4}  |
| Faces | {7} |
| Vertex figure | {4,3} |
| Dual | {3,4,7} |
| Coxeter group | [7,4,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-3 heptagonal honeycomb or 7,4,3 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-4 heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-4-3 heptagonal honeycomb is {7,4,3}, with three order-4 heptagonal tilings meeting at each edge. The vertex figure of this honeycomb is a cube, {4,3}.
 Poincaré disk model (Vertex centered) |  Ideal surface |
| Order-4-3 octagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {8,4,3} |
| Coxeter diagram |  |
| Cells | {8,4}  |
| Faces | {8} |
| Vertex figure | {4,3} |
| Dual | {3,4,8} |
| Coxeter group | [8,4,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-3 octagonal honeycomb or 8,4,3 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-4 octagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-4-3 octagonal honeycomb is {8,4,3}, with three order-4 octagonal tilings meeting at each edge. The vertex figure of this honeycomb is a cube, {4,3}.
 Poincaré disk model (Vertex centered) |
| Order-4-3 apeirogonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {∞,4,3} |
| Coxeter diagram |  |
| Cells | {∞,4}  |
| Faces | Apeirogon {∞} |
| Vertex figure | {4,3} |
| Dual | {3,4,∞} |
| Coxeter group | [∞,4,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-4-3 apeirogonal honeycomb or ∞,4,3 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an apeirogonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the apeirogonal tiling honeycomb is {∞,4,3}, with three apeirogonal tilings meeting at each edge. The vertex figure of this honeycomb is a cube, {4,3}.
The "ideal surface" projection below is a plane-at-infinity, in the Poincaré half-space model of H3. It shows an Apollonian gasket pattern of circles inside a largest circle.
 Poincaré disk model (Vertex centered) |  Ideal surface |
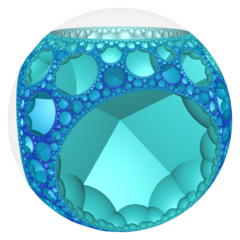
The order-6 cubic honeycomb is a paracompact regular space-filling tessellation in hyperbolic 3-space. It is paracompact because it has vertex figures composed of an infinite number of facets, with all vertices as ideal points at infinity. With Schläfli symbol {4,3,6}, the honeycomb has six ideal cubes meeting along each edge. Its vertex figure is an infinite triangular tiling. Its dual is the order-4 hexagonal tiling honeycomb.
In the field of hyperbolic geometry, the order-6 hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells with an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.
In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.
In the geometry of hyperbolic 3-space, the order-4 square tiling honeycomb is one of 11 paracompact regular honeycombs. It is paracompact because it has infinite cells and vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {4,4,4}, it has four square tilings around each edge, and infinite square tilings around each vertex in a square tiling vertex figure.
In the geometry of hyperbolic 3-space, the heptagonal tiling honeycomb or 7,3,3 honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-7 cubic honeycomb is a regular space-filling tessellation. With Schläfli symbol {4,3,7}, it has seven cubes {4,3} around each edge. All vertices are ultra-ideal with infinitely many cubes existing around each vertex in an order-7 triangular tiling vertex arrangement.
In the geometry of hyperbolic 3-space, the order-3-4 heptagonal honeycomb or 7,3,4 honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-3-5 heptagonal honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-3-6 heptagonal honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-3-7 heptagonal honeycomb a regular space-filling tessellation with Schläfli symbol {7,3,7}.
In the geometry of hyperbolic 3-space, the order-4-4 pentagonal honeycomb a regular space-filling tessellation. Each infinite cell consists of a pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-5-3 square honeycomb or 4,5,3 honeycomb a regular space-filling tessellation. Each infinite cell consists of a pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-4-5 pentagonal honeycomb a regular space-filling tessellation with Schläfli symbol {5,4,5}.
In the geometry of hyperbolic 3-space, the order-5-4 square honeycomb a regular space-filling tessellation with Schläfli symbol {4,5,4}.
In the geometry of hyperbolic 3-space, the order-7-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,7,3}.
In the geometry of hyperbolic 3-space, the order-6-3 square honeycomb or 4,6,3 honeycomb is a regular space-filling tessellation. Each infinite cell consists of a hexagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-6-4 square honeycomb a regular space-filling tessellation with Schläfli symbol {4,6,4}.
In the geometry of hyperbolic 3-space, the order-8-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,8,3}.
In the geometry of hyperbolic 3-space, the order-infinite-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,∞,3}.