
In set theory, a limit ordinal is an ordinal number that is neither zero nor a successor ordinal. Alternatively, an ordinal λ is a limit ordinal if there is an ordinal less than λ, and whenever β is an ordinal less than λ, then there exists an ordinal γ such that β < γ < λ. Every ordinal number is either zero, or a successor ordinal, or a limit ordinal.
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set that represents the result of the operation or by using transfinite recursion. Cantor normal form provides a standardized way of writing ordinals. In addition to these usual ordinal operations, there are also the "natural" arithmetic of ordinals and the nimber operations.
In mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like addition and multiplication. The original epsilon numbers were introduced by Georg Cantor in the context of ordinal arithmetic; they are the ordinal numbers ε that satisfy the equation
Gentzen's consistency proof is a result of proof theory in mathematical logic, published by Gerhard Gentzen in 1936. It shows that the Peano axioms of first-order arithmetic do not contain a contradiction, as long as a certain other system used in the proof does not contain any contradictions either. This other system, today called "primitive recursive arithmetic with the additional principle of quantifier-free transfinite induction up to the ordinal ε0", is neither weaker nor stronger than the system of Peano axioms. Gentzen argued that it avoids the questionable modes of inference contained in Peano arithmetic and that its consistency is therefore less controversial.
In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal notations. However, it is not possible to decide effectively whether a given putative ordinal notation is a notation or not ; various more-concrete ways of defining ordinals that definitely have notations are available.
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. If theories have the same proof-theoretic ordinal they are often equiconsistent, and if one theory has a larger proof-theoretic ordinal than another it can often prove the consistency of the second theory.
In mathematics, particularly set theory, non-recursive ordinals are large countable ordinals greater than all the recursive ordinals, and therefore can not be expressed using recursive ordinal notations.
In mathematics, the Feferman–Schütte ordinal (Γ0) is a large countable ordinal. It is the proof-theoretic ordinal of several mathematical theories, such as arithmetical transfinite recursion. It is named after Solomon Feferman and Kurt Schütte, the former of whom suggested the name Γ0.
In set theory and computability theory, Kleene's is a canonical subset of the natural numbers when regarded as ordinal notations. It contains ordinal notations for every computable ordinal, that is, ordinals below Church–Kleene ordinal, . Since is the first ordinal not representable in a computable system of ordinal notations the elements of can be regarded as the canonical ordinal notations.
In mathematics, the small Veblen ordinal is a certain large countable ordinal, named after Oswald Veblen. It is occasionally called the Ackermann ordinal, though the Ackermann ordinal described by Ackermann (1951) is somewhat smaller than the small Veblen ordinal.
In mathematics, the large Veblen ordinal is a certain large countable ordinal, named after Oswald Veblen.
In mathematics, the Veblen functions are a hierarchy of normal functions, introduced by Oswald Veblen in Veblen (1908). If φ0 is any normal function, then for any non-zero ordinal α, φα is the function enumerating the common fixed points of φβ for β<α. These functions are all normal.
In mathematics, the Ackermann ordinal is a certain large countable ordinal, named after Wilhelm Ackermann. The term "Ackermann ordinal" is also occasionally used for the small Veblen ordinal, a somewhat larger ordinal.
In mathematical logic and set theory, an ordinal collapsing function is a technique for defining certain recursive large countable ordinals, whose principle is to give names to certain ordinals much larger than the one being defined, perhaps even large cardinals, and then "collapse" them down to a system of notations for the sought-after ordinal. For this reason, ordinal collapsing functions are described as an impredicative manner of naming ordinals.
In computability theory, computational complexity theory and proof theory, a fast-growing hierarchy is an ordinal-indexed family of rapidly increasing functions fα: N → N. A primary example is the Wainer hierarchy, or Löb–Wainer hierarchy, which is an extension to all α < ε0. Such hierarchies provide a natural way to classify computable functions according to rate-of-growth and computational complexity.
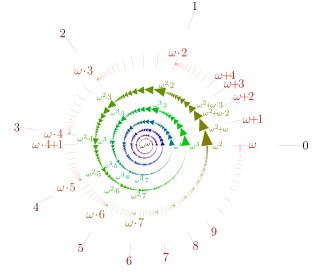
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
This is a glossary of terms and definitions related to the topic of set theory.
Buchholz's psi-functions are a hierarchy of single-argument ordinal functions introduced by German mathematician Wilfried Buchholz in 1986. These functions are a simplified version of the -functions, but nevertheless have the same strength as those. Later on this approach was extended by Jäger and Schütte.
In the mathematical fields of set theory and proof theory, the Takeuti–Feferman–Buchholz ordinal (TFBO) is a large countable ordinal, which acts as the limit of the range of Buchholz's psi function and Feferman's theta function. It was named by David Madore, after Gaisi Takeuti, Solomon Feferman and Wilfried Buchholz. It is written as using Buchholz's psi function, an ordinal collapsing function invented by Wilfried Buchholz, and in Feferman's theta function, an ordinal collapsing function invented by Solomon Feferman. It is the proof-theoretic ordinal of several formal theories:
In set theory, a mathematical discipline, a fundamental sequence is a cofinal sequence of ordinals all below a given limit ordinal. Depending on author, fundamental sequences may be restricted to ω-sequences only or permit fundamental sequences of length . The element of the fundamental sequence of is commonly denoted , although it may be denoted or . Additionally, some authors may allow fundamental sequences to be defined on successor ordinals. The term dates back to Veblen's construction of normal functions , while the concept dates back to Hardy's 1904 attempt to construct a set of cardinality .


























