
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, which gives an equal perceived step size as pitch is perceived roughly as the logarithm of frequency.

In music, there are two common meanings for tuning:
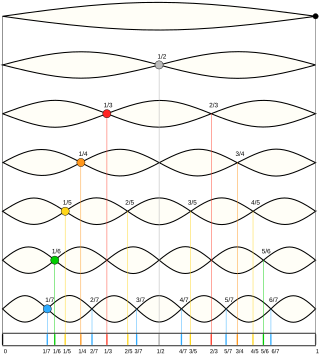
A harmonic is a wave with a frequency that is a positive integer multiple of the fundamental frequency, the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the 1st harmonic, the other harmonics are known as higher harmonics. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a harmonic series.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

Music theory is the study of the practices and possibilities of music. The Oxford Companion to Music describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation ; the second is learning scholars' views on music from antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built."

In music, timbre, also known as tone color or tone quality, is the perceived sound quality of a musical note, sound or tone. Timbre distinguishes different types of sound production, such as choir voices and musical instruments. It also enables listeners to distinguish different instruments in the same category.

In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths.. If C is chosen as a starting point, the sequence is: C, G, D, A, E, B, F♯, C♯, A♭, E♭, B♭, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle.

In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term limit was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name.

Xenharmonic music is music that uses a tuning system that is unlike the 12-tone equal temperament scale. It was named by Ivor Darreg, from Xenia, hospitable, and Xenos foreign. He stated that it was "intended to include just intonation and such temperaments as the 5-, 7-, and 11-tone, along with the higher-numbered really-microtonal systems as far as one wishes to go."

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

In classical music, a third is a musical interval encompassing three staff positions, and the major third is a third spanning four semitones. Along with the minor third, the major third is one of two commonly occurring thirds. It is qualified as major because it is the larger of the two: the major third spans four semitones, the minor third three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones.
The intervals from the tonic (keynote) in an upward direction to the second, to the third, to the sixth, and to the seventh scale degrees of a major scale are called major.

In music, consonance and dissonance are categorizations of simultaneous or successive sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness, unpleasantness, or unacceptability, although there is broad acknowledgement that this depends also on familiarity and musical expertise. The terms form a structural dichotomy in which they define each other by mutual exclusion: a consonance is what is not dissonant, and a dissonance is what is not consonant. However, a finer consideration shows that the distinction forms a gradation, from the most consonant to the most dissonant. In casual discourse, as German composer and music theorist Paul Hindemith stressed, "The two concepts have never been completely explained, and for a thousand years the definitions have varied". The term sonance has been proposed to encompass or refer indistinctly to the terms consonance and dissonance.
George Secor was an American musician, composer and music-theorist from Chicago. He was the discoverer of miracle temperament and eponym of the secor.
Twelve-tone equal temperament (12-TET) is the musical system that divides the octave into 12 parts, all of which are equally tempered on a logarithmic scale, with a ratio equal to the 12th root of 2. That resulting smallest interval, 1⁄12 the width of an octave, is called a semitone or half step.

A neutral third is a musical interval wider than a minor third play (help·info) but narrower than a major third play (help·info), named by Jan Pieter Land in 1880. Land makes reference to the neutral third attributed to Zalzal, described by Al-Farabi as corresponding to a ratio of 27:22 and by Avicenna as 39:32. The Zalzalian third may have been a mobile interval.
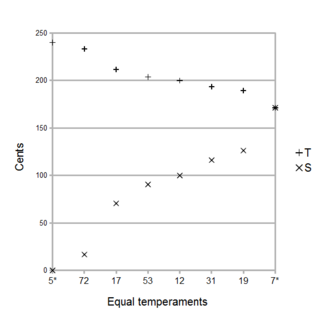
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.
Dynamic tonality is a paradigm for tuning and timbre which generalizes the special relationship between just intonation and the harmonic series to apply to a wider set of pseudo-just tunings and related pseudo-harmonic timbres.
William A. Sethares is an American music theorist and professor of electrical engineering at the University of Wisconsin. In music, he has contributed to the theory of Dynamic Tonality and provided a formalization of consonance.
Post-tonal music theory is the set of theories put forward to describe music written outside of, or 'after', the tonal system of the common practice period. It revolves around the idea of 'emancipating dissonance', that is, freeing the structure of music from the familiar harmonic patterns that are derived from natural overtones. As music becomes more complex, dissonance becomes indistinguishable from consonance.
Kees (Cornelis) van Prooijen is a creator of computer art. Although it does not bear his name, he independently discovered the Bohlen-Pierce scale, a non-octave-repeating scale based on the tritave and spectra containing odd harmonics, in 1978. Van Prooijen came across the scale through an investigation of continued fractions.

 4:5:6 (help·info),
4:5:6 (help·info),  6:7:9 (help·info), and
6:7:9 (help·info), and 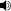 10:12:15 (help·info). See full resolution for locations of the triads on the plot
10:12:15 (help·info). See full resolution for locations of the triads on the plot






















