
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero, i.e., 0 K. Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which microscopic quantum-mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. More generally, condensation refers to the appearance of macroscopic occupation of one or several states: for example, in BCS theory, a superconductor is a condensate of Cooper pairs. As such, condensation can be associated with phase transition, and the macroscopic occupation of the state is the order parameter.
Superfluid helium-4 is the superfluid form of helium-4, an isotope of the element helium. A superfluid is a state of matter in which matter behaves like a fluid with zero viscosity. The substance, which resembles other liquids such as helium I, flows without friction past any surface, which allows it to continue to circulate over obstructions and through pores in containers which hold it, subject only to its own inertia.

In physics, polaritons are bosonic quasiparticles resulting from strong coupling of electromagnetic waves (photon) with an electric or magnetic dipole-carrying excitation (state) of solid or liquid matter. Polaritons describe the crossing of the dispersion of light with any interacting resonance.
In condensed matter physics, a Cooper pair or BCS pair is a pair of electrons bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper.
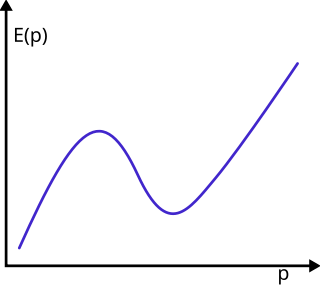
In theoretical physics, a roton is an elementary excitation, or quasiparticle, seen in superfluid helium-4 and Bose–Einstein condensates with long-range dipolar interactions or spin-orbit coupling. The dispersion relation of elementary excitations in this superfluid shows a linear increase from the origin, but exhibits first a maximum and then a minimum in energy as the momentum increases. Excitations with momenta in the linear region are called phonons; those with momenta close to the minimum are called rotons. Excitations with momenta near the maximum are called maxons.

In condensed matter physics, a supersolid is a spatially ordered material with superfluid properties. In the case of helium-4, it has been conjectured since the 1960s that it might be possible to create a supersolid. Starting from 2017, a definitive proof for the existence of this state was provided by several experiments using atomic Bose–Einstein condensates. The general conditions required for supersolidity to emerge in a certain substance are a topic of ongoing research.
In condensed matter physics, a quasiparticle is a concept used to describe a collective behavior of a group of particles that can be treated as if they were a single particle. Formally, quasiparticles and collective excitations are closely related phenomena that arise when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in vacuum.
Cryogenic particle detectors operate at very low temperature, typically only a few degrees above absolute zero. These sensors interact with an energetic elementary particle and deliver a signal that can be related to the type of particle and the nature of the interaction. While many types of particle detectors might be operated with improved performance at cryogenic temperatures, this term generally refers to types that take advantage of special effects or properties occurring only at low temperature.

In physics, a quantum vortex represents a quantized flux circulation of some physical quantity. In most cases, quantum vortices are a type of topological defect exhibited in superfluids and superconductors. The existence of quantum vortices was first predicted by Lars Onsager in 1949 in connection with superfluid helium. Onsager reasoned that quantisation of vorticity is a direct consequence of the existence of a superfluid order parameter as a spatially continuous wavefunction. Onsager also pointed out that quantum vortices describe the circulation of superfluid and conjectured that their excitations are responsible for superfluid phase transitions. These ideas of Onsager were further developed by Richard Feynman in 1955 and in 1957 were applied to describe the magnetic phase diagram of type-II superconductors by Alexei Alexeyevich Abrikosov. In 1935 Fritz London published a very closely related work on magnetic flux quantization in superconductors. London's fluxoid can also be viewed as a quantum vortex.
A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.
In condensed matter physics, second sound is a quantum mechanical phenomenon in which heat transfer occurs by wave-like motion, rather than by the more usual mechanism of diffusion. Its presence leads to a very high thermal conductivity. It is known as "second sound" because the wave motion of entropy and temperature is similar to the propagation of pressure waves in air (sound). The phenomenon of second sound was first described by Lev Landau in 1941.
Helium atom scattering (HAS) is a surface analysis technique used in materials science. It provides information about the surface structure and lattice dynamics of a material by measuring the diffracted atoms from a monochromatic helium beam incident on the sample.
In theoretical physics, the logarithmic Schrödinger equation is one of the nonlinear modifications of Schrödinger's equation, first proposed by Gerald H. Rosen in its relativistic version in 1969. It is a classical wave equation with applications to extensions of quantum mechanics, quantum optics, nuclear physics, transport and diffusion phenomena, open quantum systems and information theory, effective quantum gravity and physical vacuum models and theory of superfluidity and Bose–Einstein condensation. It is an example of an integrable model.
Adrian Frederick George Wyatt, FRS is a British physicist, and Emeritus Professor at University of Exeter. He is a member of the Quantum Systems and Nanomaterials group. He won the 2004 Fernand Holweck Medal and Prize of the Institute of Physics.

Superfluidity is the characteristic property of a fluid with zero viscosity which therefore flows without any loss of kinetic energy. When stirred, a superfluid forms vortices that continue to rotate indefinitely. Superfluidity occurs in two isotopes of helium when they are liquefied by cooling to cryogenic temperatures. It is also a property of various other exotic states of matter theorized to exist in astrophysics, high-energy physics, and theories of quantum gravity. The theory of superfluidity was developed by Soviet theoretical physicists Lev Landau and Isaak Khalatnikov.

In the field of cryogenics, helium [He] is utilized for a variety of reasons. The combination of helium’s extremely low molecular weight and weak interatomic reactions yield interesting properties when helium is cooled below its critical temperature of 5.2 K to form a liquid. Even at absolute zero (0K), helium does not condense to form a solid under ambient pressure. In this state, the zero point vibrational energies of helium are comparable to very weak interatomic binding interactions, thus preventing lattice formation and giving helium its fluid characteristics. Within this liquid state, helium has two phases referred to as helium I and helium II. Helium I displays thermodynamic and hydrodynamic properties of classical fluids, along with quantum characteristics. However, below its lambda point of 2.17 K, helium transitions to He II and becomes a quantum superfluid with zero viscosity.

Giorgio Benedek is an Italian physicist, academic and researcher. He is an Emeritus Professor of Physics of Matter at University of Milano-Bicocca and Director of the International School of Solid State Physics at Ettore Majorana Foundation and Centre for Scientific Culture.

An electron-on-helium qubit is a quantum bit for which the orthonormal basis states |0⟩ and |1⟩ are defined by quantized motional states or alternatively the spin states of an electron trapped above the surface of liquid helium. The electron-on-helium qubit was proposed as the basic element for building quantum computers with electrons on helium by Platzman and Dykman in 1999.
GrigoryEfimovich Volovik is a Russian theoretical physicist, who specializes in condensed matter physics. He is known for the Volovik effect.

Victor S. L'vov is a Russian-Israeli physicist most known for his contributions to the advanced theories and applications of wave and hydrodynamic turbulence, as well as nonlinear phenomena in various physical systems, including plasma, superfluids, classical environmental flows, and solid states. He has authored about 280 publications in academic journals, including Nature Physics and Physical Review, and has written three books: Nonlinear Spin Waves, Kolmogorov Spectra of Turbulence I: Wave Turbulence, and Wave Turbulence under Parametric Excitation: Applications to Magnets.










