Mechanism
In conducting and semi-conducting materials, changes in inter-atomic spacing resulting from strain affect the bandgaps, making it easier (or harder depending on the material and strain) for electrons to be raised into the conduction band. This results in a change in resistivity of the material. Within a certain range of strain this relationship is linear, so that the piezoresistive coefficient

where
- ∂ρ = Change in resistivity
- ρ = Original resistivity
- ε = Strain
are constant.
Usually the resistance change in metals is mostly due to the change of geometry resulting from applied mechanical stress. However, even though the piezoresistive effect is small in those cases it is often not negligible. In cases where it is, it can be calculated using the simple resistance equation derived from Ohm's law;

where
 Conductor length [m]
Conductor length [m]- A Cross-sectional area of the current flow [m2] [2] : p.207
Some metals display piezoresistivity that is much larger than the resistance change due to geometry. In platinum alloys, for instance, piezoresistivity is more than a factor of two larger, combining with the geometry effects to give a strain gauge sensitivity of up to more than three times as large than due to geometry effects alone. Pure nickel's piezoresistivity is -13 times larger, completely dwarfing and even reversing the sign of the geometry-induced resistance change.
Piezoresistive effect in bulk semiconductors
The piezoresistive effect of semiconductor materials can be several orders of magnitudes larger than the geometrical effect and is present in materials like germanium, polycrystalline silicon, amorphous silicon, silicon carbide, and single crystal silicon. Hence, semiconductor strain gauges with a very high coefficient of sensitivity can be built. For precision measurements they are more difficult to handle than metal strain gauges, because semiconductor strain gauges are generally sensitive to environmental conditions (especially temperature).
For silicon, gauge factors can be two orders of magnitudes larger than those observed in most metals (Smith 1954). The resistance of n-conducting silicon mainly changes due to a shift of the three different conducting valley pairs. The shifting causes a redistribution of the carriers between valleys with different mobilities. This results in varying mobilities dependent on the direction of current flow. A minor effect is due to the effective mass change related to changing shapes of the valleys. In p-conducting silicon the phenomena are more complex and also result in mass changes and hole transfer.
A giant piezoresistive effect – where the piezoresistive coefficient exceeds the bulk value – was reported for a microfabricated silicon-aluminium hybrid structure. [3] The effect has been applied to silicon-based sensor technologies. [4]
Giant piezoresistive effect in silicon nanostructures
The longitudinal piezoresistive coefficient of top-down fabricated silicon nanowires was measured to be 60% larger than in bulk silicon. [5] [6] In 2006, giant piezoresistance [7] was reported in bottom-up fabricated silicon nanowires – a >30 increase in the longitudinal piezoresistive coefficient compared to bulk silicon was reported. The suggestion of a giant piezoresistance in nanostructures has since stimulated much effort into a physical understanding of the effect not only in silicon [8] [9] [10] [11] [12] [13] [14] but also in other functional materials. [15]
Piezoresistive silicon devices
The piezoresistive effect of semiconductors has been used for sensor devices employing all kinds of semiconductor materials such as germanium, polycrystalline silicon, amorphous silicon, and single crystal silicon. Since silicon is today the material of choice for integrated digital and analog circuits the use of piezoresistive silicon devices has been of great interest. It enables the easy integration of stress sensors with Bipolar and CMOS circuits.
This has enabled a wide range of products using the piezoresistive effect. Many commercial devices such as pressure sensors and acceleration sensors employ the piezoresistive effect in silicon. But due to its magnitude the piezoresistive effect in silicon has also attracted the attention of research and development for all other devices using single crystal silicon. Semiconductor Hall sensors, for example, were capable of achieving their current precision only after employing methods which eliminate signal contributions due to applied mechanical stress.
Piezoresistors
Piezoresistors are resistors made from a piezoresistive material and are usually used for measurement of mechanical stress. They are the simplest form of piezoresistive devices.
Fabrication
Piezoresistors can be fabricated using wide variety of piezoresistive materials. The simplest form of piezoresistive silicon sensors are diffused resistors. Piezoresistors consist of a simple two contact diffused n- or p-wells within a p- or n-substrate. As the typical square resistances of these devices are in the range of several hundred ohms, additional p+ or n+ plus diffusions are a potential method to facilitate ohmic contacts to the device.
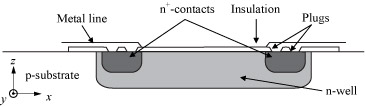
Schematic cross-section of the basic elements of a silicon n-well piezoresistor.
Physics of operation
For typical stress values in the MPa range the stress dependent voltage drop along the resistor Vr, can be considered to be linear. A piezoresistor aligned with the x-axis as shown in the figure may be described by

where  , I,
, I,  ,
,  , and
, and  denote the stress free resistance, the applied current, the transverse and longitudinal piezoresistive coefficients, and the three tensile stress components, respectively. The piezoresistive coefficients vary significantly with the sensor orientation with respect to the crystallographic axes and with the doping profile. Despite the fairly large stress sensitivity of simple resistors, they are preferably used in more complex configurations eliminating certain cross sensitivities and drawbacks. Piezoresistors have the disadvantage of being highly sensitive to temperature changes while featuring comparatively small relative stress dependent signal amplitude changes.
denote the stress free resistance, the applied current, the transverse and longitudinal piezoresistive coefficients, and the three tensile stress components, respectively. The piezoresistive coefficients vary significantly with the sensor orientation with respect to the crystallographic axes and with the doping profile. Despite the fairly large stress sensitivity of simple resistors, they are preferably used in more complex configurations eliminating certain cross sensitivities and drawbacks. Piezoresistors have the disadvantage of being highly sensitive to temperature changes while featuring comparatively small relative stress dependent signal amplitude changes.
This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.








