Related Research Articles

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

In crystallography, a crystal system is a set of point groups. A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family.
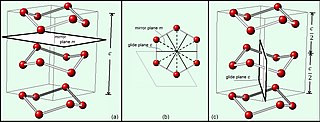
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.
In crystallography, a crystallographic point group is a set of symmetry operations, corresponding to one of the point groups in three dimensions, such that each operation would leave the structure of a crystal unchanged i.e. the same kinds of atoms would be placed in similar positions as before the transformation. For example, in many crystals in the cubic crystal system, a rotation of the unit cell by 90 degrees around an axis that is perpendicular to one of the faces of the cube is a symmetry operation that moves each atom to the location of another atom of the same kind, leaving the overall structure of the crystal unaffected.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length. There are four types: translations, rotations, reflections, and glide reflections.

Crystal twinning occurs when two or more adjacent crystals of the same mineral are oriented so that they share some of the same crystal lattice points in a symmetrical manner. The result is an intergrowth of two separate crystals that are tightly bonded to each other. The surface along which the lattice points are shared in twinned crystals is called a composition surface or twin plane.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.
In geometry and crystallography, a glide plane is a symmetry operation describing how a reflection in a plane, followed by a translation parallel with that plane, may leave the crystal unchanged.
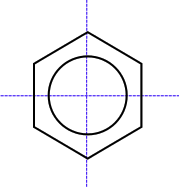
In crystallography, a centrosymmetric point group contains an inversion center as one of its symmetry elements. In such a point group, for every point in the unit cell there is an indistinguishable point. Such point groups are also said to have inversion symmetry. Point reflection is a similar term used in geometry. Crystals with an inversion center cannot display certain properties, such as the piezoelectric effect.

A screw axis is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis.

In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.
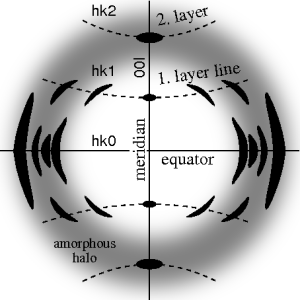
Fiber diffraction is a subarea of scattering, an area in which molecular structure is determined from scattering data. In fiber diffraction the scattering pattern does not change, as the sample is rotated about a unique axis. Such uniaxial symmetry is frequent with filaments or fibers consisting of biological or man-made macromolecules. In crystallography fiber symmetry is an aggravation regarding the determination of crystal structure, because reflexions are smeared and may overlap in the fiber diffraction pattern. Materials science considers fiber symmetry a simplification, because almost the complete obtainable structure information is in a single two-dimensional (2D) diffraction pattern exposed on photographic film or on a 2D detector. 2 instead of 3 co-ordinate directions suffice to describe fiber diffraction.
In crystallography, a Wyckoff position is any point in a set of points whose site symmetry groups are all conjugate subgroups one of another. Crystallography tables give the Wyckoff positions for different space groups.
In chemistry and crystallography, a symmetry element is a point, line, or plane about which symmetry operations can take place. In particular, a symmetry element can be a mirror plane, an axis of rotation, or a center of inversion. For an object such as a molecule or a crystal, a symmetry element corresponds to a set of symmetry operations, which are the rigid transformations employing the symmetry element that leave the object unchanged. The set containing these operations form one of the symmetry groups of the object. The elements of this symmetry group should not to be confused with the "symmetry element" itself. Loosely, a symmetry element is the geometric set of fixed points of a symmetry operation. For example, for rotation about an axis, the points on the axis do not move and in a reflection the points that remain unchanged make up a plane of symmetry.
In group theory, geometry, representation theory and molecular geometry, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, as transformations of an object in space, rotations, reflections and inversions are all symmetry operations. Such symmetry operations are performed with respect to symmetry elements. In the context of molecular symmetry, a symmetry operation is a permutation of atoms such that the molecule or crystal is transformed into a state indistinguishable from the starting state. Two basic facts follow from this definition, which emphasizes its usefulness.
- Physical properties must be invariant with respect to symmetry operations.
- Symmetry operations can be collected together in groups which are isomorphic to permutation groups.

In chemistry, molecular symmetry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical properties, such as whether or not it has a dipole moment, as well as its allowed spectroscopic transitions. To do this it is necessary to use group theory. This involves classifying the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Symmetry is useful in the study of molecular orbitals, with applications to the Hückel method, to ligand field theory, and to the Woodward-Hoffmann rules. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry discuss symmetry. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials.

In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.
References
- 1 2 Jeremy Karl Cockcroft; Huub Driessen; David Moss; Ian Tickle (2006). "Polar Point Groups". University of London. Retrieved 2013-12-09.
- ↑ Kasap, Safa O. (2006). Principles of electronic materials and devices. Boston: McGraw-Hill. ISBN 978-0-07-310464-5.
- ↑ Zink, Jeffery (1981). "Triboluminescence-Structure Relations in Polymorphs of Hexaphenylcarbodiphosphorane and Anthranilic Acid, Molecular Crystals, and Salts". J. Am. Chem. Soc. 103: 1074–1079. doi:10.1021/ja00395a014.