
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter k and a scale parameter θ
- With a shape parameter and an inverse scale parameter , called a rate parameter.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

Lagrange's four-square theorem, also known as Bachet's conjecture, states that every natural number can be represented as a sum of four non-negative integer squares. That is, the squares form an additive basis of order four. where the four numbers are integers. For illustration, 3, 31, and 310 in several ways, can be represented as the sum of four squares as follows:
The Cayley–Purser algorithm was a public-key cryptography algorithm published in early 1999 by 16-year-old Irishwoman Sarah Flannery, based on an unpublished work by Michael Purser, founder of Baltimore Technologies, a Dublin data security company. Flannery named it for mathematician Arthur Cayley. It has since been found to be flawed as a public-key algorithm, but was the subject of considerable media attention.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
In mathematics, Hensel's lemma, also known as Hensel's lifting lemma, named after Kurt Hensel, is a result in modular arithmetic, stating that if a univariate polynomial has a simple root modulo a prime number p, then this root can be lifted to a unique root modulo any higher power of p. More generally, if a polynomial factors modulo p into two coprime polynomials, this factorization can be lifted to a factorization modulo any higher power of p.

In mathematics, the Eisenstein integers, occasionally also known as Eulerian integers, are the complex numbers of the form
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
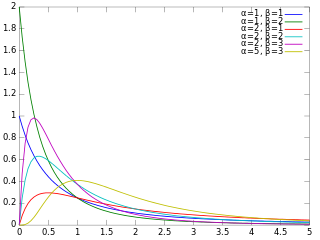
In probability theory and statistics, the beta prime distribution is an absolutely continuous probability distribution. If has a beta distribution, then the odds has a beta prime distribution.
Continuous wavelets of compact support alpha can be built, which are related to the beta distribution. The process is derived from probability distributions using blur derivative. These new wavelets have just one cycle, so they are termed unicycle wavelets. They can be viewed as a soft variety of Haar wavelets whose shape is fine-tuned by two parameters and . Closed-form expressions for beta wavelets and scale functions as well as their spectra are derived. Their importance is due to the Central Limit Theorem by Gnedenko and Kolmogorov applied for compactly supported signals.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.

The multivariate stable distribution is a multivariate probability distribution that is a multivariate generalisation of the univariate stable distribution. The multivariate stable distribution defines linear relations between stable distribution marginals. In the same way as for the univariate case, the distribution is defined in terms of its characteristic function.
In mathematics, the Perrin numbers are a doubly infinite constant-recursive integer sequence with characteristic equation x3 = x + 1. The Perrin numbers bear the same relationship to the Padovan sequence as the Lucas numbers do to the Fibonacci sequence.
In mathematics, the Kodaira–Spencer map, introduced by Kunihiko Kodaira and Donald C. Spencer, is a map associated to a deformation of a scheme or complex manifold X, taking a tangent space of a point of the deformation space to the first cohomology group of the sheaf of vector fields on X.
The Einstein–Hilbert action for general relativity was first formulated purely in terms of the space-time metric. To take the metric and affine connection as independent variables in the action principle was first considered by Palatini. It is called a first order formulation as the variables to vary over involve only up to first derivatives in the action and so doesn't overcomplicate the Euler–Lagrange equations with higher derivative terms. The tetradic Palatini action is another first-order formulation of the Einstein–Hilbert action in terms of a different pair of independent variables, known as frame fields and the spin connection. The use of frame fields and spin connections are essential in the formulation of a generally covariant fermionic action which couples fermions to gravity when added to the tetradic Palatini action.
The cyclotomic fast Fourier transform is a type of fast Fourier transform algorithm over finite fields. This algorithm first decomposes a DFT into several circular convolutions, and then derives the DFT results from the circular convolution results. When applied to a DFT over , this algorithm has a very low multiplicative complexity. In practice, since there usually exist efficient algorithms for circular convolutions with specific lengths, this algorithm is very efficient.

In theoretical physics, the dual graviton is a hypothetical elementary particle that is a dual of the graviton under electric-magnetic duality, as an S-duality, predicted by some formulations of eleven-dimensional supergravity.
This article summarizes several identities in exterior calculus, a mathematical notation used in differential geometry.
















































