In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
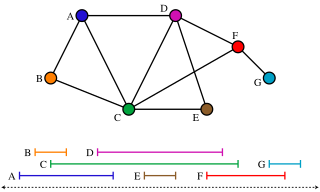
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

In graph theory, a circle graph is the intersection graph of a chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.
In graph theory, Schnyder's theorem is a characterization of planar graphs in terms of the order dimension of their incidence posets. It is named after Walter Schnyder, who published its proof in 1989.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices; thus, it can be described as "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.
In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

In graph theory, a mathematical discipline, a factor-critical graph is a graph with n vertices in which every induced subgraph of n − 1 vertices has a perfect matching.
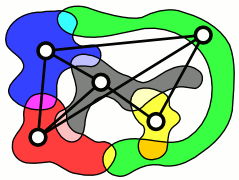
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
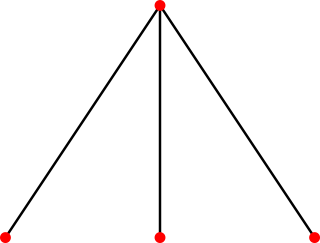
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.
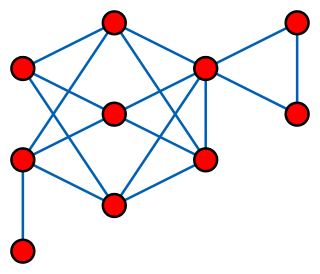
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In the mathematical field of graph theory, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.
In the study of graph algorithms, an implicit graph representation is a graph whose vertices or edges are not represented as explicit objects in a computer's memory, but rather are determined algorithmically from some other input, for example a computable function.
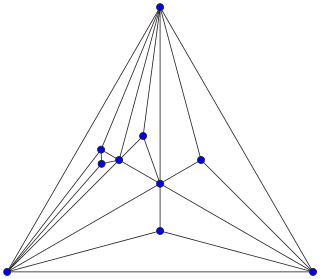
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

Layered graph drawing or hierarchical graph drawing is a type of graph drawing in which the vertices of a directed graph are drawn in horizontal rows or layers with the edges generally directed downwards. It is also known as Sugiyama-style graph drawing after Kozo Sugiyama, who first developed this drawing style.

In geometric graph theory, a penny graph is a contact graph of unit circles. It is formed from a collection of unit circles that do not cross each other, by creating a vertex for each circle and an edge for every pair of tangent circles. The circles can be represented physically by pennies, arranged without overlapping on a flat surface, with a vertex for each penny and an edge for each two pennies that touch.














