Probability distribution of extreme points of a Wiener stochastic process

In the mathematical theory of probability, the Wiener process, named after Norbert Wiener, is a stochastic process used in modeling various phenomena, including Brownian motion and fluctuations in financial markets. A formula for the conditional probability distribution of the extremum of the Wiener process and a sketch of its proof appears in work of H. J. Kusher (appendix 3, page 106) published in 1964. ^[1] a detailed constructive proof appears in work of Dario Ballabio in 1978. ^[2] This result was developed within a research project about Bayesian optimization algorithms.

In some global optimization problems the analytical definition of the objective function is unknown and it is only possible to get values at fixed points. There are objective functions in which the cost of an evaluation is very high, for example when the evaluation is the result of an experiment or a particularly onerous measurement. In these cases, the search of the global extremum (maximum or minimum) can be carried out using a methodology named "Bayesian optimization", which tend to obtain a priori the best possible result with a predetermined number of evaluations. In summary it is assumed that outside the points in which it has already been evaluated, the objective function has a pattern which can be represented by a stochastic process with appropriate characteristics. The stochastic process is taken as a model of the objective function, assuming that the probability distribution of its extrema gives the best indication about extrema of the objective function. In the simplest case of the one-dimensional optimization, given that the objective function has been evaluated in a number of points, there is the problem to choose in which of the intervals thus identified is more appropriate to invest in a further evaluation. If a Wiener stochastic process is chosen as a model for the objective function, it is possible to calculate the probability distribution of the model extreme points inside each interval, conditioned by the known values at the interval boundaries. The comparison of the obtained distributions provides a criterion for selecting the interval in which the process should be iterated. The probability value of having identified the interval in which falls the global extremum point of the objective function can be used as a stopping criterion. Bayesian optimization is not an efficient method for the accurate search of local extrema so, once the search range has been restricted, depending on the characteristics of the problem, a specific local optimization method can be used.

Proposition

Let ${\displaystyle X(t)}$ be a Wiener stochastic process on an interval ${\displaystyle [a,b]}$ with initial value ${\displaystyle X(a)=X_{a}.}$

By definition of Wiener process, increments have a normal distribution:

${\displaystyle {\text{for }}a\leq t_{1}<t_{2}\leq b,\qquad X(t_{2})-X(t_{1})\sim N(0,\sigma ^{2}(t_{2}-t_{1})).}$

Let

${\displaystyle F(z)=\Pr(\min _{a\leq t\leq b}X(t)\leq z\mid X(b)=X_{b})}$

be the cumulative probability distribution function of the minimum value of the ${\displaystyle X(t)}$ function on interval ${\displaystyle [a,b]}$ conditioned by the value ${\displaystyle X(b)=X_{b}.}$

It is shown that: ^{[1] [3] [note 1]}

${\displaystyle F(z)={\begin{cases}1&{\text{for }}z\geq \min\{X_{a},X_{b}\},\\\exp \left(-2{\dfrac {(z-X_{b})(z-X_{a})}{\sigma ^{2}(b-a)}}\right)&{\text{for }}z<\min(X_{a},X_{b}).\end{cases}}}$

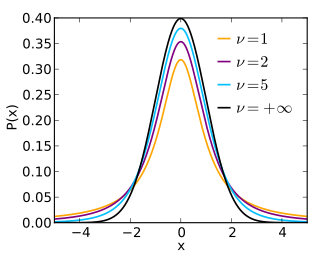
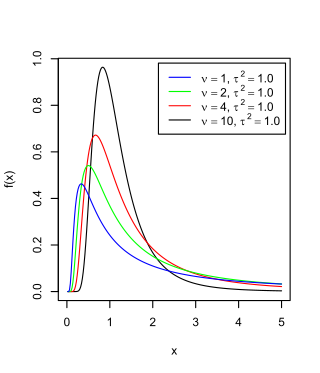
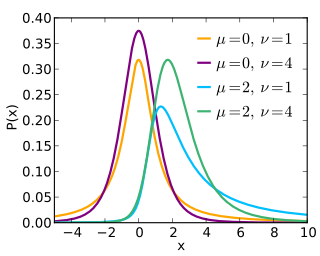
Constructive proof

Case ${\displaystyle z\geq \min(X_{a},X_{b})}$ is an immediate consequence of the minimum definition, in the following it will always be assumed ${\displaystyle z<\min(X_{a},X_{b})}$ and also corner case ${\displaystyle \min _{a\leq t\leq b}X(t)=\min(X_{a},X_{b})}$ will be excluded.

Let' s assume ${\displaystyle X(t)}$ defined in a finite number of points ${\displaystyle t_{k}\in [a,b],\ \ 0\leq k\leq n,\ \ t_{0}=a}$.

Let ${\displaystyle T_{n}\ \ {\overset {\underset {\mathrm {def} }{}}{=}}\ \ \{t_{k},\ \ 0\leq k\leq n,\}}$ by varying the integer ${\displaystyle n}$ be a sequence of sets ${\displaystyle \{T_{n}\}}$ such that ${\displaystyle T_{n}\subset T_{n+1}}$ and ${\displaystyle \bigcup _{n=0}^{+\infty }T_{n}}$ be a dense set in ${\displaystyle [a,b]}$,

hence every neighbourhood of each point in ${\displaystyle [a,b]}$ contains an element of one of the sets ${\displaystyle T_{n}}$.

Let ${\displaystyle \Delta z}$ be a real positive number such that ${\displaystyle z+\Delta z<\min(X_{a},X_{b}).}$

Let the event ${\displaystyle E}$ be defined as: ${\displaystyle E\ \ {\overset {\underset {\mathrm {def} }{}}{=}}\ \ (\min _{a\leq t\leq b}X(t)<z+\Delta z)}$${\displaystyle \Longleftrightarrow }$${\displaystyle (\exists \,t\in [a,b]:X(t)<z+\Delta z)}$ .

Having excluded corner case ${\displaystyle \min _{a\leq t\leq b}X(t)=\min(X_{a},X_{b})}$, it is surely ${\displaystyle P(E)>0}$.

Let ${\displaystyle E_{n},\ \ n=0,1,2,\ldots }$ be the events defined as: ${\displaystyle E_{n}\ \ {\overset {\underset {\mathrm {def} }{}}{=}}\ \ (\exists \,t_{k}\in T_{n}:z<X(t_{k})<z+\Delta z)}$ and let ${\displaystyle \nu }$ be the first k among the ${\displaystyle t_{k}\in T_{n}}$ which define ${\displaystyle E_{n}}$ .

Since ${\displaystyle T_{n}\subset T_{n+1}}$ it is evidently ${\displaystyle E_{n}\subset E_{n+1}}$. Now equation (2.1) will be proved.

(2.1)${\displaystyle \ \ \ \ E=\bigcup _{n=0}^{+\infty }E_{n}}$

By the ${\displaystyle E_{n}}$ events definition,${\displaystyle \forall \,n\ \ E_{n}\Rightarrow E}$, hence ${\displaystyle \bigcup _{n=0}^{+\infty }E_{n}\subset E}$ . It will now be verified the relation ${\displaystyle E\subset \bigcup _{n=0}^{+\infty }E_{n}}$ hence (2.1) will be proved.

The definition of ${\displaystyle E}$, the continuity of ${\displaystyle X(t)}$ and the hypothesis ${\displaystyle z<X_{a}=X(a)}$ imply, by the intermediate value theorem, ${\displaystyle (\exists \,{\bar {t}}\in [a,b]:z<X({\bar {t}})<z+\Delta z)}$.

By the continuity of ${\displaystyle X(t)}$ and the hypothesis that ${\displaystyle \bigcup _{n=0}^{+\infty }T_{n}}$ is dense in ${\displaystyle [a,b]}$ it is deducted that ${\displaystyle \exists \,{\bar {n}}}$ such that for ${\displaystyle t_{\nu }\in T_{\bar {n}}}$ it must be ${\displaystyle z<X(t_{\nu })<z+\Delta z}$ ,

hence ${\displaystyle E\subset E_{\bar {n}}\subset \bigcup _{n=0}^{+\infty }E_{n}}$ which implies (2.1).

(2.2)${\displaystyle \ \ \ \ P(E)=\lim _{n\rightarrow +\infty }P(E_{n})}$

(2.2) is deducted from (2.1), considering that ${\displaystyle E_{n}\Rightarrow E_{n+1}}$ implies that the sequence of probabilities ${\displaystyle P(E_{n})}$ is monotone non decreasing and hence it converges to its supremum. The definition of events ${\displaystyle E_{n}}$ implies ${\displaystyle \forall n\ \ P(E_{n})>0\Rightarrow P(E_{n})=P(E_{\nu })}$ and (2.2) implies ${\displaystyle P(E)=P(E_{\nu })}$.

In the following it will always be assumed ${\displaystyle n\geq \nu }$, so ${\displaystyle t_{\nu }}$ is well defined.

(2.3)${\displaystyle \ \ \ \ P(X(b)\leqslant -X_{b}+2z)\leqslant P(X(b)-X(t_{\nu })<-X_{b}+z)}$

In fact, by definition of ${\displaystyle E_{n}}$ it is ${\displaystyle z<X(t_{\nu })}$, so ${\displaystyle (X(b)\leqslant -X_{b}+2z)\Rightarrow (X(b)-X(t_{\nu })<-X_{b}+z)}$.

In a similar way, since by definition of ${\displaystyle E_{n}}$ it is ${\displaystyle z<X(t_{\nu })}$, (2.4) is valid:

(2.4)${\displaystyle \ \ \ \ P(X(b)-X(t_{\nu })>X_{b}-z)\leqslant P(X(b)>X_{b})}$

(2.5)${\displaystyle \ \ \ \ P(X(b)-X(t_{\nu })<-X_{b}+z)=P(X(b)-X(t_{\nu })>X_{b}-z)}$

The above is explained by the fact that the random variable ${\displaystyle (X(b)-X(t_{\nu }))\thicksim N(\varnothing$ ;\ \ \sigma ^{2}(b-t_{\nu }))} has a symmetric probability density compared to its mean which is zero.

By applying in sequence relationships (2.3), (2.5) and (2.4) we get (2.6) :

(2.6)${\displaystyle \ \ \ \ P(X(b)\leqslant -X_{b}+2z)\leqslant P(X(b)>X_{b})}$

With the same procedure used to obtain (2.3), (2.4) and (2.5) taking advantage this time by the relationship ${\displaystyle X(t_{\nu })<z+\Delta z}$ we get (2.7):

(2.7)${\displaystyle \ \ \ \ P(X(b)>X_{b})\leqslant P(X(b)-X(t_{\nu })>X_{b}-z-\Delta z)\ \ }$${\displaystyle =\ \ P(X(b)-X(t_{\nu })<-X_{b}+z+\Delta z)\leqslant P(X(b)<-X_{b}+2z+2\Delta z)}$

By applying in sequence (2.6) and (2.7) we get:

(2.8)${\displaystyle P(X(b)\leqslant -X_{b}+2z)\leqslant P(X(b)>X_{b})}$${\displaystyle \leqslant P(X(b)<-X_{b}+2z+2\Delta z)}$

From ${\displaystyle X_{b}>z+\Delta z>z}$, considering the continuity of ${\displaystyle X(t)}$ and the intermediate value theorem we get ${\displaystyle X(b)>X_{b}>z+\Delta z>z\Rightarrow E_{n}}$ ,

which implies ${\displaystyle P(X(b)>X_{b})=P(E_{n},X(b)>X_{b})}$.

Replacing the above in (2.8) and passing to the limits: ${\displaystyle \lim _{n\rightarrow +\ \infty }\ \ E_{n}(\Delta z)\rightarrow E(\Delta z)}$ and for ${\displaystyle \Delta z\rightarrow 0}$, event ${\displaystyle E(\Delta z)}$ converges to ${\displaystyle \min _{a\leq t\leq b}X(t)\leqslant z}$

(2.9)${\displaystyle \ \ \ \ P(X(b)\leqslant -X_{b}+2z)=}$${\displaystyle P(\min _{a\leq t\leq b}X(t)\leqslant z,\ \ X(b)>X_{b})}$

${\displaystyle \forall \,dX_{b}>0}$, by substituting ${\displaystyle (X_{b})}$ with ${\displaystyle (X_{b}-dX_{b})}$ in (2.9) we get the equivalent relationship:

(2.10)${\displaystyle \ \ \ \ P(X(b)\leqslant -X_{b}+2z+dX_{b})=}$${\displaystyle P(\min _{a\leq t\leq b}X(t)\leqslant z,\ \ X(b)>X_{b}-dX_{b})}$

Applying the Bayes' theorem to the joint event ${\displaystyle (\min _{a\leq t\leq b}X(t)\leqslant z,\ \ X_{b}-dX_{b}<X(b)\leqslant X_{b})}$

(2.11)${\displaystyle \ \ \ \ P(\min _{a\leq t\leq b}X(t)\leqslant z\mid X_{b}-dX_{b}<X(b)\leqslant X_{b})=}$${\displaystyle P(\min _{a\leq t\leq b}X(t)\leqslant z,\ \ X_{b}-dX_{b}<X(b)\leqslant X_{b})}$${\displaystyle /\ \ P(X_{b}-dX_{b}<X(b)\leqslant X_{b})}$

Let: ${\displaystyle B\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{X(b)>X_{b}\},\ C\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{X_{b}-dX_{b}<X(b)\leq X_{b}\},\ D\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{X(b)>X_{b}-dX_{b}\},\ A\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \ \{\min _{a\leq t\leq b}X(t)\leqslant z\}}$From the above definitions it follows:

${\displaystyle D=B\cup C\Rightarrow \ P(A,D)=P(A,B\cup C)=P(A,B)+P(A,C)\Rightarrow P(A,C)=P(A,D)-P(A,B)}$

(2.12)${\displaystyle \ \ \ \ P(A,C)=P(A,D)-P(A,B)}$

Substituting (2.12) into (2.11), we get the equivalent:

(2.13)${\displaystyle P(\min _{a\leq t\leq b}X(t)\leqslant z\mid X_{b}-dX_{b}<X(b)\leqslant X_{b})=(P(\min _{a\leqslant t\leqslant b}X(t)\leq z,\ \ X(b)>X_{b}-dX_{b})-P(\min _{a\leqslant t\leqslant b}X(t)\leq z,\ \ X(b)>X_{b}))\ \ /\ \ P(X_{b}-dX_{b}<X(b)\leqslant X_{b})}$

Substituting (2.9) and (2.10) into (2.13):

(2.14)${\displaystyle \ \ \ \ P(\min _{a\leq t\leq b}X(t)\leqslant z\mid X_{b}-dX_{b}<X(b)\leqslant X_{b})=}$${\displaystyle (P(X(b)\leqslant -X_{b}+2z+dX_{b})-P(X(b)\leqslant -X_{b}+2z)}$${\displaystyle /\ \ P(X_{b}-dX_{b}<X(b)\leqslant X_{b})}$

It can be observed that in the second member of (2.14) appears the probability distribution of the random variable ${\displaystyle X(b)}$, normal with mean ${\displaystyle X_{a}}$ e variance ${\displaystyle \sigma ^{2}(b-a)}$.

The realizations ${\displaystyle X_{b}}$ and ${\displaystyle -X_{b}+2z}$ of the random variable ${\displaystyle X(b)}$ match respectively the probability densities:

(2.15)${\displaystyle \ \ \ \ P(X_{b})\,dX_{b}={\frac {1}{\sigma {\sqrt {2\pi (b-a)}}}}\exp {\biggl (}-{\frac {1}{2}}{\frac {(X_{b}-X_{a})^{2}}{\sigma ^{2}(b-a)}}{\biggr )}\,dX_{b}}$

(2.16)${\displaystyle \ \ \ \ P(-X_{b}+2z)\,dX_{b}={\frac {1}{\sigma {\sqrt {2\pi (b-a)}}}}\exp {\biggl (}-{\frac {1}{2}}{\frac {(-X_{b}+2z-X_{a})^{2}}{\sigma ^{2}(b-a)}}{\biggr )}\,dX_{b}}$

Substituting (2.15) e (2.16) into (2.14) and taking the limit for ${\displaystyle dX_{b}\rightarrow 0}$ the thesis is proved:

${\displaystyle F(z)=P(\min _{a\leq t\leq b}X(t)\leq z\ \ |\ \ X(b)=X_{b})=}$

${\displaystyle ={\frac {1}{\sigma {\sqrt {2\pi (b-a)}}}}\exp {\biggl (}-{\frac {1}{2}}{\frac {(-X_{b}+2z-X_{a})^{2}}{\sigma ^{2}(b-a)}}{\biggr )}\,dX_{b}}$${\displaystyle \ \ \diagup \ \ {\frac {1}{\sigma {\sqrt {2\pi (b-a)}}}}\exp {\biggl (}-{\frac {1}{2}}{\frac {(X_{b}-X_{a})^{2}}{\sigma ^{2}(b-a)}}{\biggr )}\,dX_{b}=}$

${\displaystyle =\exp {\biggl (}-{\frac {1}{2}}{\frac {(-X_{b}+2z-X_{a})^{2}-(X_{b}-X_{a})^{2}}{\sigma ^{2}(b-a)}}{\biggr )}=}$${\displaystyle \ \ \exp {\biggl (}-2\ \ {\frac {(z-X_{b})(z-X_{a})}{\sigma ^{2}(b-a)}}{\biggr )}}$

Bibliography

• A versatile stochastic model of a function of unknown and time varying form - Harold J Kushner - Journal of Mathematical Analysis and Applications Volume 5, Issue 1, August 1962, Pages 150-167.
• The Application of Bayesian Methods for Seeking the Extremum - J. Mockus, J. Tiesis, A. Zilinskas - IFIP Congress 1977, August 8–12 Toronto.

See also

• Random variable
• Probability
• Event (probability theory)
• Conditional probability
• Regular conditional probability
• Stochastic process
• Wiener process

Notes

1. The theorem, as set out and shown for the case of the minimum of the Wiener process, also applies to the maximum.

References

1. H. J. Kushner, "A New Method of Locating the Maximum Point of an Arbitrary Multipeak Curve in the Presence of Noise", J. Basic Eng 86(1), 97–106 (Mar 01, 1964).
2. Dario Ballabio, "Una nuova classe di algoritmi stocastici per l'ottimizzazione globale" (A new class of stochastic algorithms for global optimization), University of Milan, Institute of Mathematics, doctoral dissertation presented on July 12th 1978, pp. 29–33.
3. János D. Pintér, Global Optimization in Action: Continuous and Lipschitz Optimization, 1996 Springer Science & Business Media, page 57.