In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms. Quadratus is Latin for square.
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer coefficients. For example, the golden ratio, , is an algebraic number, because it is a root of the polynomial x2 − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x4 + 4.
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.
In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.
In algebra, a quadratic equation is any equation that can be rearranged in standard form as
In mathematics, a square root of a number x is a number y such that ; in other words, a number y whose square is x. For example, 4 and −4 are square roots of 16 because .
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.
In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is an integer factorization of 15, and (x – 2)(x + 2) is a polynomial factorization of x2 – 4.
In algebra, a cubic equation in one variable is an equation of the form
In mathematics, a quadratic form is a polynomial with terms all of degree two. For example,
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
In mathematics, an expression is in closed form if it is formed with constants, variables and a finite set of basic functions connected by arithmetic operations and function composition. Commonly, the allowed functions are nth root, exponential function, logarithm, and trigonometric functions. However, the set of basic functions depends on the context.
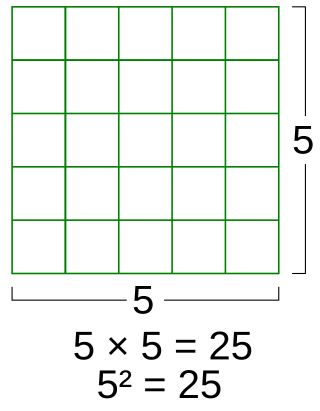
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.
The following outline is provided as an overview of and topical guide to algebra:
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a special symbol, or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as e and π occurring in such diverse contexts as geometry, number theory, statistics, and calculus.
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.