
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a nucleus of a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.
Spontaneous emission is the process in which a quantum mechanical system transits from an excited energy state to a lower energy state and emits a quantized amount of energy in the form of a photon. Spontaneous emission is ultimately responsible for most of the light we see all around us; it is so ubiquitous that there are many names given to what is essentially the same process. If atoms are excited by some means other than heating, the spontaneous emission is called luminescence. For example, fireflies are luminescent. And there are different forms of luminescence depending on how excited atoms are produced. If the excitation is effected by the absorption of radiation the spontaneous emission is called fluorescence. Sometimes molecules have a metastable level and continue to fluoresce long after the exciting radiation is turned off; this is called phosphorescence. Figurines that glow in the dark are phosphorescent. Lasers start via spontaneous emission, then during continuous operation work by stimulated emission.

The active laser medium is the source of optical gain within a laser. The gain results from the stimulated emission of photons through electronic or molecular transitions to a lower energy state from a higher energy state previously populated by a pump source.

A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle in physics, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves.
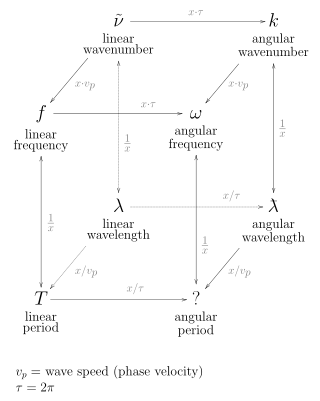
In the physical sciences, the wavenumber, also known as repetency, is the spatial frequency of a wave, measured in cycles per unit distance or radians per unit distance. It is analogous to temporal frequency, which is defined as the number of wave cycles per unit time or radians per unit time.
In spectroscopy, the Rydberg constant, symbol for heavy atoms or for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants according to his model of the atom.
In atomic physics, a dark state refers to a state of an atom or molecule that cannot absorb photons. All atoms and molecules are described by quantum states; different states can have different energies and a system can make a transition from one energy level to another by emitting or absorbing one or more photons. However, not all transitions between arbitrary states are allowed. A state that cannot absorb an incident photon is called a dark state. This can occur in experiments using laser light to induce transitions between energy levels, when atoms can spontaneously decay into a state that is not coupled to any other level by the laser light, preventing the atom from absorbing or emitting light from that state.

In physics, the Lamb shift, named after Willis Lamb, is an anomalous difference in energy between two electron orbitals in a hydrogen atom. The difference was not predicted by theory and it cannot be derived from the Dirac equation, which predicts identical energies. Hence the Lamb shift is a deviation from theory seen in the differing energies contained by the 2S1/2 and 2P1/2 orbitals of the hydrogen atom.
The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was instead a set of heuristic corrections to classical mechanics. The theory has come to be understood as the semi-classical approximation to modern quantum mechanics. The main and final accomplishments of the old quantum theory were the determination of the modern form of the periodic table by Edmund Stoner and the Pauli exclusion principle which were both premised on the Arnold Sommerfeld enhancements to the Bohr model of the atom.
In physics, tunnel ionization is a process in which electrons in an atom tunnel through the potential barrier and escape from the atom. In an intense electric field, the potential barrier of an atom (molecule) is distorted drastically. Therefore, as the length of the barrier that electrons have to pass decreases, the electrons can escape from the atom's potential more easily. Tunneling ionization is a quantum mechanical phenomenon since in the classical picture an electron does not have sufficient energy to overcome the potential barrier of the atom.

A Rydberg atom is an excited atom with one or more electrons that have a very high principal quantum number, n. The higher the value of n, the farther the electron is from the nucleus, on average. Rydberg atoms have a number of peculiar properties including an exaggerated response to electric and magnetic fields, long decay periods and electron wavefunctions that approximate, under some conditions, classical orbits of electrons about the nuclei. The core electrons shield the outer electron from the electric field of the nucleus such that, from a distance, the electric potential looks identical to that experienced by the electron in a hydrogen atom.
Quantum noise is noise arising from the indeterminate state of matter in accordance with fundamental principles of quantum mechanics, specifically the uncertainty principle and via zero-point energy fluctuations. Quantum noise is due to the apparently discrete nature of the small quantum constituents such as electrons, as well as the discrete nature of quantum effects, such as photocurrents.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
In spectroscopy, the Autler–Townes effect, is a dynamical Stark effect corresponding to the case when an oscillating electric field is tuned in resonance to the transition frequency of a given spectral line, and resulting in a change of the shape of the absorption/emission spectra of that spectral line. The AC Stark effect was discovered in 1955 by American physicists Stanley Autler and Charles Townes.
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.
The Kapitza–Dirac effect is a quantum mechanical effect consisting of the diffraction of matter by a standing wave of light. The effect was first predicted as the diffraction of electrons from a standing wave of light by Paul Dirac and Pyotr Kapitsa in 1933. The effect relies on the wave–particle duality of matter as stated by the de Broglie hypothesis in 1924.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.

In quantum optics, a superradiant phase transition is a phase transition that occurs in a collection of fluorescent emitters, between a state containing few electromagnetic excitations and a superradiant state with many electromagnetic excitations trapped inside the emitters. The superradiant state is made thermodynamically favorable by having strong, coherent interactions between the emitters.
In quantum mechanics, magnetic resonance is a resonant effect that can appear when a magnetic dipole is exposed to a static magnetic field and perturbed with another, oscillating electromagnetic field. Due to the static field, the dipole can assume a number of discrete energy eigenstates, depending on the value of its angular momentum (azimuthal) quantum number. The oscillating field can then make the dipole transit between its energy states with a certain probability and at a certain rate. The overall transition probability will depend on the field's frequency and the rate will depend on its amplitude. When the frequency of that field leads to the maximum possible transition probability between two states, a magnetic resonance has been achieved. In that case, the energy of the photons composing the oscillating field matches the energy difference between said states. If the dipole is tickled with a field oscillating far from resonance, it is unlikely to transition. That is analogous to other resonant effects, such as with the forced harmonic oscillator. The periodic transition between the different states is called Rabi cycle and the rate at which that happens is called Rabi frequency. The Rabi frequency should not be confused with the field's own frequency. Since many atomic nuclei species can behave as a magnetic dipole, this resonance technique is the basis of nuclear magnetic resonance, including nuclear magnetic resonance imaging and nuclear magnetic resonance spectroscopy.




















