
Linear algebra is the branch of mathematics concerning linear equations such as:

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Euclidean vectors can be added and scaled to form a vector space. A vector quantity is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a directed line segment. A vector is frequently depicted graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by
In mathematics, hypercomplex number is a traditional term for an element of a finite-dimensional unital algebra over the field of real numbers. The study of hypercomplex numbers in the late 19th century forms the basis of modern group representation theory.

In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by H, or in blackboard bold by Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form

Hermann Günther Grassmann was a German polymath known in his day as a linguist and now also as a mathematician. He was also a physicist, general scholar, and publisher. His mathematical work was little noted until he was in his sixties. His work preceded and exceeded the concept which is now known as a vector space. He introduced the Grassmannian, the space which parameterizes all k-dimensional linear subspaces of an n-dimensional vector space V. In linguistics he helped free language history and structure from each other.
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

Christian Hugo Eduard Study was a German mathematician known for work on invariant theory of ternary forms (1889) and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.

Alexander Macfarlane FRSE LLD was a Scottish logician, physicist, and mathematician.
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form
Alexander McAulay was the first professor of mathematics and physics at the University of Tasmania, Hobart, Tasmania. He was also a proponent of dual quaternions, which he termed "octonions" or "Clifford biquaternions".
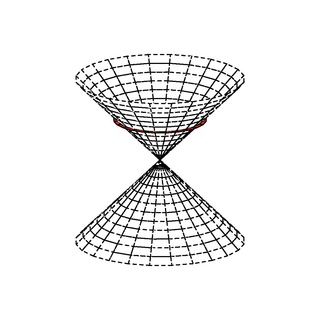
In mathematics, given a vector space X with an associated quadratic form q, written (X, q), a null vector or isotropic vector is a non-zero element x of X for which q(x) = 0.
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.
In mathematics, a versor is a quaternion of norm one. Each versor has the form
Cargill Gilston Knott FRS, FRSE LLD was a Scottish physicist and mathematician who was a pioneer in seismological research. He spent his early career in Japan. He later became a Fellow of the Royal Society, Secretary of the Royal Society of Edinburgh, and President of the Scottish Meteorological Society.
A non-associative algebra (or distributive algebra) is an algebra over a field where the binary multiplication operation is not assumed to be associative. That is, an algebraic structure A is a non-associative algebra over a field K if it is a vector space over K and is equipped with a K-bilinear binary multiplication operation A × A → A which may or may not be associative. Examples include Lie algebras, Jordan algebras, the octonions, and three-dimensional Euclidean space equipped with the cross product operation. Since it is not assumed that the multiplication is associative, using parentheses to indicate the order of multiplications is necessary. For example, the expressions (ab)(cd), (a(bc))d and a(b(cd)) may all yield different answers.

In mathematics, quaternions are a non-commutative number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations.

A History of Vector Analysis (1967) is a book on the history of vector analysis by Michael J. Crowe, originally published by the University of Notre Dame Press. As a scholarly treatment of a reformation in technical communication, the text is a contribution to the history of science. In 2002, Crowe gave a talk summarizing the book, including an entertaining introduction in which he covered its publication history and related the award of a Jean Scott prize of $4000. Crowe had entered the book in a competition for "a study on the history of complex and hypercomplex numbers" twenty-five years after his book was first published.
In mathematics and physics, vector is a term that refers to quantities that cannot be expressed by a single number, or to elements of some vector spaces. They have to be expressed by both magnitude and direction.
In mathematics, hypercomplex analysis is the extension of complex analysis to the hypercomplex numbers. The first instance is functions of a quaternion variable, where the argument is a quaternion. A second instance involves functions of a motor variable where arguments are split-complex numbers.

Hüseyin Tevfik Pasha was a mathematician from the Ottoman Empire and military adjutant representing the Ottoman Empire in the purchase of foreign rifles. He is remembered for his Linear Algebra which outlined some vector algebra including a "special perpendicular" and properties of curves. The book title was precocious since the early vector algebra was generalized in vector space, and this concept later produced linear algebra. He is known as Tawfiq Pasha of Vidin or as Vidinli Huseyin, Tawfiq Pasha in Turkish literature. He served as Envoy of the Ottoman Empire to the United States.