In computer science, an array is a data structure consisting of a collection of elements, each identified by at least one array index or key. An array is stored such that the position of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called one-dimensional array.
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
In computer science, a data structure is a data organization, management, and storage format that is usually chosen for efficient access to data. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data, i.e., it is an algebraic structure about data.
In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
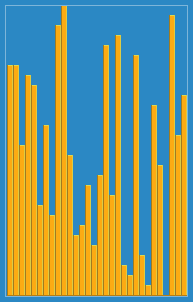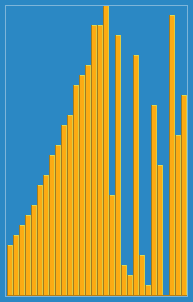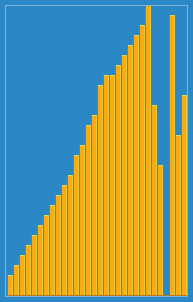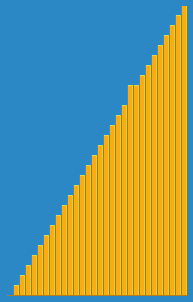
Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains: data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that access time is linear. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.
In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.
Sequential access is a term describing a group of elements being accessed in a predetermined, ordered sequence. It is the opposite of random access, the ability to access an arbitrary element of a sequence as easily and efficiently as any other at any time.
In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.
In computer programming, a reference is a value that enables a program to indirectly access a particular data, such as a variable's value or a record, in the computer's memory or in some other storage device. The reference is said to refer to the datum, and accessing the datum is called dereferencing the reference. A reference is distinct from the datum itself.
In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".
In computing, a persistent data structure or not ephemeral data structure is a data structure that always preserves the previous version of itself when it is modified. Such data structures are effectively immutable, as their operations do not (visibly) update the structure in-place, but instead always yield a new updated structure. The term was introduced in Driscoll, Sarnak, Sleator, and Tarjans' 1986 article.
In computer science, data is any sequence of one or more symbols; datum is a single symbol of data. Data requires interpretation to become information. Digital data is data that is represented using the binary number system of ones (1) and zeros (0), instead of analog representation. In modern (post-1960) computer systems, all data is digital.
In computer science, an implicit data structure or space-efficient data structure is a data structure that stores very little information other than the main or required data: a data structure that requires low overhead. They are called "implicit" because the position of the elements carries meaning and relationship between elements; this is contrasted with the use of pointers to give an explicit relationship between elements. Definitions of "low overhead" vary, but generally means constant overhead; in big O notation, O(1) overhead. A less restrictive definition is a succinct data structure, which allows greater overhead.
A sorted array is an array data structure in which each element is sorted in numerical, alphabetical, or some other order, and placed at equally spaced addresses in computer memory. It is typically used in computer science to implement static lookup tables to hold multiple values which have the same data type. Sorting an array is useful in organising data in ordered form and recovering them rapidly.
In computer science, the all nearest smaller values problem is the following task: for each position in a sequence of numbers, search among the previous positions for the last position that contains a smaller value. This problem can be solved efficiently both by parallel and non-parallel algorithms: Berkman, Schieber & Vishkin (1993), who first identified the procedure as a useful subroutine for other parallel programs, developed efficient algorithms to solve it in the Parallel Random Access Machine model; it may also be solved in linear time on a non-parallel computer using a stack-based algorithm. Later researchers have studied algorithms to solve it in other models of parallel computation.
In computer science, a linked data structure is a data structure which consists of a set of data records (nodes) linked together and organized by references. The link between data can also be called a connector.
In computer science, a search data structure is any data structure that allows the efficient retrieval of specific items from a set of items, such as a specific record from a database.
In computing, sequence containers refer to a group of container class templates in the standard library of the C++ programming language that implement storage of data elements. Being templates, they can be used to store arbitrary elements, such as integers or custom classes. One common property of all sequential containers is that the elements can be accessed sequentially. Like all other standard library components, they reside in namespace std.
