
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

A random variable is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' can be misleading as it is not actually random or a variable, but rather it is a mapping or a function from possible outcomes in a sample space to a measurable space, often to the real numbers.
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's seed. Although sequences that are closer to truly random can be generated using hardware random number generators, pseudorandom number generators are important in practice for their speed in number generation and their reproducibility.
The Mersenne Twister is a general-purpose pseudorandom number generator (PRNG) developed in 1997 by Makoto Matsumoto and Takuji Nishimura. Its name derives from the fact that its period length is chosen to be a Mersenne prime.
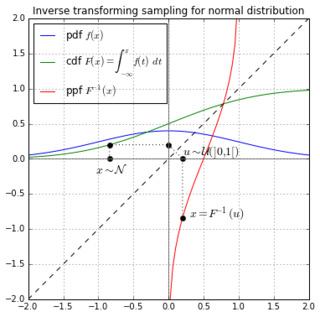
Inverse transform sampling is a basic method for pseudo-random number sampling, i.e., for generating sample numbers at random from any probability distribution given its cumulative distribution function.

The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller, is a random number sampling method for generating pairs of independent, standard, normally distributed random numbers, given a source of uniformly distributed random numbers. The method was in fact first mentioned explicitly by Raymond E. A. C. Paley and Norbert Wiener in 1934.
A random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation. A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.

Random number generation is a process by which, often by means of a random number generator (RNG), a sequence of numbers or symbols that cannot be reasonably predicted better than by random chance is generated. This means that the particular outcome sequence will contain some patterns detectable in hindsight but unpredictable to foresight. True random number generators can be hardware random-number generators (HRNGs), wherein each generation is a function of the current value of a physical environment's attribute that is constantly changing in a manner that is practically impossible to model. This would be in contrast to so-called "random number generations" done by pseudorandom number generators (PRNGs), which generate numbers that only look random but are in fact pre-determined—these generations can be reproduced simply by knowing the state of the PRNG.
Slice sampling is a type of Markov chain Monte Carlo algorithm for pseudo-random number sampling, i.e. for drawing random samples from a statistical distribution. The method is based on the observation that to sample a random variable one can sample uniformly from the region under the graph of its density function.

In probability and statistics, a realization, observation, or observed value, of a random variable is the value that is actually observed. The random variable itself is the process dictating how the observation comes about. Statistical quantities computed from realizations without deploying a statistical model are often called "empirical", as in empirical distribution function or empirical probability.
In statistics and computer software, a convolution random number generator is a pseudo-random number sampling method that can be used to generate random variates from certain classes of probability distribution. The particular advantage of this type of approach is that it allows advantage to be taken of existing software for generating random variates from other, usually non-uniform, distributions. However, faster algorithms may be obtainable for the same distributions by other more complicated approaches.
A standard normal deviate is a normally distributed deviate. It is a realization of a standard normal random variable, defined as a random variable with expected value 0 and variance 1. Where collections of such random variables are used, there is often an associated assumption that members of such collections are statistically independent.
In computer science and probability theory, a random binary tree is a binary tree selected at random from some probability distribution on binary trees. Two different distributions are commonly used: binary trees formed by inserting nodes one at a time according to a random permutation, and binary trees chosen from a uniform discrete distribution in which all distinct trees are equally likely. It is also possible to form other distributions, for instance by repeated splitting. Adding and removing nodes directly in a random binary tree will in general disrupt its random structure, but the treap and related randomized binary search tree data structures use the principle of binary trees formed from a random permutation in order to maintain a balanced binary search tree dynamically as nodes are inserted and deleted.
Non-uniform random variate generation or pseudo-random number sampling is the numerical practice of generating pseudo-random numbers (PRN) that follow a given probability distribution. Methods are typically based on the availability of a uniformly distributed PRN generator. Computational algorithms are then used to manipulate a single random variate, X, or often several such variates, into a new random variate Y such that these values have the required distribution. The first methods were developed for Monte-Carlo simulations in the Manhattan project, published by John von Neumann in the early 1950s.
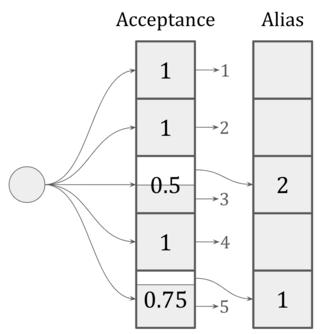
In computing, the alias method is a family of efficient algorithms for sampling from a discrete probability distribution, published in 1974 by A. J. Walker. That is, it returns integer values 1 ≤ i ≤ n according to some arbitrary probability distribution pi. The algorithms typically use O(n log n) or O(n) preprocessing time, after which random values can be drawn from the distribution in O(1) time.





