Rho (Ρ or ρ) is a letter of the Greek alphabet.
Contents
Rho or RHO also may refer to:
Rho (Ρ or ρ) is a letter of the Greek alphabet.
Rho or RHO also may refer to:
Density is a substance's mass per unit of volume. The symbol most often used for density is ρ, although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume: where ρ is the density, m is the mass, and V is the volume. In some cases, density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight.
In physics, specifically statistical mechanics, an ensemble is an idealization consisting of a large number of virtual copies of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902.
Electrical resistivity is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). For example, if a 1 m3 solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.

In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are linearly related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve.

In thermodynamics and fluid mechanics, the compressibility is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure change. In its simple form, the compressibility may be expressed as
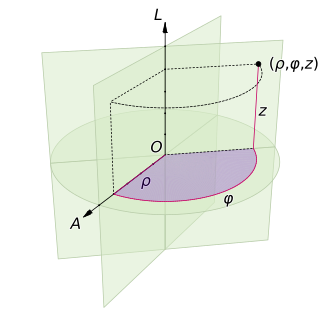
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.

A solenoid is a type of electromagnet formed by a helical coil of wire whose length is substantially greater than its diameter, which generates a controlled magnetic field. The coil can produce a uniform magnetic field in a volume of space when an electric current is passed through it.

In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a primary school to have a Pearson correlation coefficient significantly greater than 0, but less than 1.

In statistics, Spearman's rank correlation coefficient or Spearman's ρ, named after Charles Spearman and often denoted by the Greek letter (rho) or as , is a nonparametric measure of rank correlation. It assesses how well the relationship between two variables can be described using a monotonic function.
Rho is the seventeenth letter of the Greek alphabet. In the system of Greek numerals it has a value of 100. It is derived from Phoenician letter res . Its uppercase form uses the same glyph, Ρ, as the distinct Latin letter P; the two letters have different Unicode encodings.

In statistics, the Fisher transformation of a Pearson correlation coefficient is its inverse hyperbolic tangent (artanh). When the sample correlation coefficient r is near 1 or -1, its distribution is highly skewed, which makes it difficult to estimate confidence intervals and apply tests of significance for the population correlation coefficient ρ. The Fisher transformation solves this problem by yielding a variable whose distribution is approximately normally distributed, with a variance that is stable over different values of r.
Greek letters are used in mathematics, science, engineering, and other areas where mathematical notation is used as symbols for constants, special functions, and also conventionally for variables representing certain quantities. In these contexts, the capital letters and the small letters represent distinct and unrelated entities. Those Greek letters which have the same form as Latin letters are rarely used: capital A, B, E, Z, H, I, K, M, N, O, P, T, Y, X. Small ι, ο and υ are also rarely used, since they closely resemble the Latin letters i, o and u. Sometimes, font variants of Greek letters are used as distinct symbols in mathematics, in particular for ε/ϵ and π/ϖ. The archaic letter digamma (Ϝ/ϝ/ϛ) is sometimes used.

In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter H, is a distance over which a physical quantity decreases by a factor of e.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation in the classical case is
Local-density approximations (LDA) are a class of approximations to the exchange–correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space. Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems.
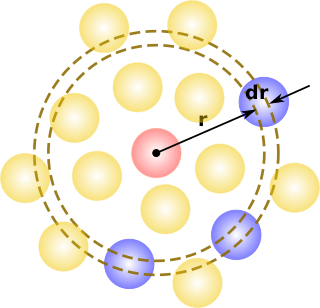
In statistical mechanics, the radial distribution function, in a system of particles, describes how density varies as a function of distance from a reference particle.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.
Lemaître coordinates are a particular set of coordinates for the Schwarzschild metric—a spherically symmetric solution to the Einstein field equations in vacuum—introduced by Georges Lemaître in 1932. Changing from Schwarzschild to Lemaître coordinates removes the coordinate singularity at the Schwarzschild radius.

The mass attenuation coefficient, or mass narrow beam attenuation coefficient of a material is the attenuation coefficient normalized by the density of the material; that is, the attenuation per unit mass. Thus, it characterizes how easily a mass of material can be penetrated by a beam of light, sound, particles, or other energy or matter. In addition to visible light, mass attenuation coefficients can be defined for other electromagnetic radiation, sound, or any other beam that can be attenuated. The SI unit of mass attenuation coefficient is the square metre per kilogram. Other common units include cm2/g and L⋅g−1⋅cm−1. Mass extinction coefficient is an old term for this quantity.
In mathematics, log-polar coordinates is a coordinate system in two dimensions, where a point is identified by two numbers, one for the logarithm of the distance to a certain point, and one for an angle. Log-polar coordinates are closely connected to polar coordinates, which are usually used to describe domains in the plane with some sort of rotational symmetry. In areas like harmonic and complex analysis, the log-polar coordinates are more canonical than polar coordinates.