
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes or metamaterials.

Structural alignment attempts to establish homology between two or more polymer structures based on their shape and three-dimensional conformation. This process is usually applied to protein tertiary structures but can also be used for large RNA molecules. In contrast to simple structural superposition, where at least some equivalent residues of the two structures are known, structural alignment requires no a priori knowledge of equivalent positions. Structural alignment is a valuable tool for the comparison of proteins with low sequence similarity, where evolutionary relationships between proteins cannot be easily detected by standard sequence alignment techniques. Structural alignment can therefore be used to imply evolutionary relationships between proteins that share very little common sequence. However, caution should be used in using the results as evidence for shared evolutionary ancestry because of the possible confounding effects of convergent evolution by which multiple unrelated amino acid sequences converge on a common tertiary structure.

Structural bioinformatics is the branch of bioinformatics that is related to the analysis and prediction of the three-dimensional structure of biological macromolecules such as proteins, RNA, and DNA. It deals with generalizations about macromolecular 3D structures such as comparisons of overall folds and local motifs, principles of molecular folding, evolution, binding interactions, and structure/function relationships, working both from experimentally solved structures and from computational models. The term structural has the same meaning as in structural biology, and structural bioinformatics can be seen as a part of computational structural biology. The main objective of structural bioinformatics is the creation of new methods of analysing and manipulating biological macromolecular data in order to solve problems in biology and generate new knowledge.
Visual Molecular Dynamics (VMD) is a molecular modelling and visualization computer program. VMD is developed mainly as a tool to view and analyze the results of molecular dynamics simulations. It also includes tools for working with volumetric data, sequence data, and arbitrary graphics objects. Molecular scenes can be exported to external rendering tools such as POV-Ray, RenderMan, Tachyon, Virtual Reality Modeling Language (VRML), and many others. Users can run their own Tcl and Python scripts within VMD as it includes embedded Tcl and Python interpreters. VMD runs on Unix, Apple Mac macOS, and Microsoft Windows. VMD is available to non-commercial users under a distribution-specific license which permits both use of the program and modification of its source code, at no charge.
In abstract algebra, the biquaternions are the numbers w + xi + yj + zk, where w, x, y, and z are complex numbers, or variants thereof, and the elements of {1, i, j, k} multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions corresponding to complex numbers and the variations thereof:
In computational phylogenetics, tree alignment is a computational problem concerned with producing multiple sequence alignments, or alignments of three or more sequences of DNA, RNA, or protein. Sequences are arranged into a phylogenetic tree, modeling the evolutionary relationships between species or taxa. The edit distances between sequences are calculated for each of the tree's internal vertices, such that the sum of all edit distances within the tree is minimized. Tree alignment can be accomplished using one of several algorithms with various trade-offs between manageable tree size and computational effort.

Multiple sequence alignment (MSA) is the process or the result of sequence alignment of three or more biological sequences, generally protein, DNA, or RNA. These alignments are used to infer evolutionary relationships via phylogenetic analysis and can highlight homologous features between sequences. Alignments highlight mutation events such as point mutations, insertion mutations and deletion mutations, and alignments are used to assess sequence conservation and infer the presence and activity of protein domains, tertiary structures, secondary structures, and individual amino acids or nucleotides.

Low-energy electron diffraction (LEED) is a technique for the determination of the surface structure of single-crystalline materials by bombardment with a collimated beam of low-energy electrons (30–200 eV) and observation of diffracted electrons as spots on a fluorescent screen.

UCSF Chimera is an extensible program for interactive visualization and analysis of molecular structures and related data, including density maps, supramolecular assemblies, sequence alignments, docking results, trajectories, and conformational ensembles. High-quality images and movies can be created. Chimera includes complete documentation and can be downloaded free of charge for noncommercial use.
Protein–ligand docking is a molecular modelling technique. The goal of protein–ligand docking is to predict the position and orientation of a ligand when it is bound to a protein receptor or enzyme. Pharmaceutical research employs docking techniques for a variety of purposes, most notably in the virtual screening of large databases of available chemicals in order to select likely drug candidates. There has been rapid development in computational ability to determine protein structure with programs such as AlphaFold, and the demand for the corresponding protein-ligand docking predictions is driving implementation of software that can find accurate models. Once the protein folding can be predicted accurately along with how the ligands of various structures will bind to the protein, the ability for drug development to progress at a much faster rate becomes possible.
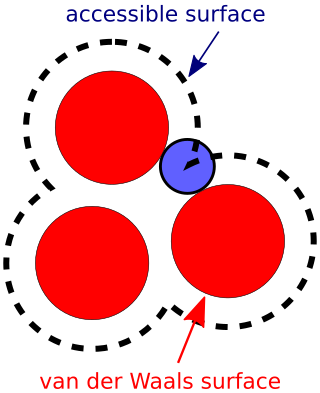
The accessible surface area (ASA) or solvent-accessible surface area (SASA) is the surface area of a biomolecule that is accessible to a solvent. Measurement of ASA is usually described in units of square angstroms. ASA was first described by Lee & Richards in 1971 and is sometimes called the Lee-Richards molecular surface. ASA is typically calculated using the 'rolling ball' algorithm developed by Shrake & Rupley in 1973. This algorithm uses a sphere of a particular radius to 'probe' the surface of the molecule.
This list of structural comparison and alignment software is a compilation of software tools and web portals used in pairwise or multiple structural comparison and structural alignment.

Half Sphere exposure (HSE) is a protein solvent exposure measure that was first introduced by Hamelryck (2005). Like all solvent exposure measures it measures how buried amino acid residues are in a protein. It is found by counting the number of amino acid neighbors within two half spheres of chosen radius around the amino acid. The calculation of HSE is found by dividing a contact number (CN) sphere in two halves by the plane perpendicular to the Cβ-Cα vector. This simple division of the CN sphere results in two strikingly different measures, HSE-up and HSE-down. HSE-up is defined as the number of Cα atoms in the upper half and analogously HSE-down is defined as the number of Cα atoms in the opposite sphere.
The global distance test (GDT), also written as GDT_TS to represent "total score", is a measure of similarity between two protein structures with known amino acid correspondences but different tertiary structures. It is most commonly used to compare the results of protein structure prediction to the experimentally determined structure as measured by X-ray crystallography, protein NMR, or, increasingly, cryoelectron microscopy.
The root mean square deviation (RMSD) or root mean square error (RMSE) is either one of two closely related and frequently used measures of the differences between true or predicted values on the one hand and observed values or an estimator on the other.
The Kabsch algorithm, also known as the Kabsch-Umeyama algorithm, named after Wolfgang Kabsch and Shinji Umeyama, is a method for calculating the optimal rotation matrix that minimizes the RMSD between two paired sets of points. It is useful for point-set registration in computer graphics, and in cheminformatics and bioinformatics to compare molecular and protein structures.
In bioinformatics, the template modeling score or TM-score is a measure of similarity between two protein structures. The TM-score is intended as a more accurate measure of the global similarity of full-length protein structures than the often used RMSD measure. The TM-score indicates the similarity between two structures by a score between , where 1 indicates a perfect match between two structures. Generally scores below 0.20 corresponds to randomly chosen unrelated proteins whereas structures with a score higher than 0.5 assume roughly the same fold. A quantitative study shows that proteins of TM-score = 0.5 have a posterior probability of 37% in the same CATH topology family and of 13% in the same SCOP fold family. The probabilities increase rapidly when TM-score > 0.5. The TM-score is designed to be independent of protein lengths.
The sequential structure alignment program (SSAP) in chemistry, physics, and biology is a method that uses double dynamic programming to produce a structural alignment based on atom-to-atom vectors in structure space. Instead of the alpha carbons typically used in structural alignment, SSAP constructs its vectors from the beta carbons for all residues except glycine, a method which thus takes into account the rotameric state of each residue as well as its location along the backbone. SSAP works by first constructing a series of inter-residue distance vectors between each residue and its nearest non-contiguous neighbors on each protein. A series of matrices are then constructed containing the vector differences between neighbors for each pair of residues for which vectors were constructed. Dynamic programming applied to each resulting matrix determines a series of optimal local alignments which are then summed into a "summary" matrix to which dynamic programming is applied again to determine the overall structural alignment.
In bioinformatics, alignment-free sequence analysis approaches to molecular sequence and structure data provide alternatives over alignment-based approaches.
SuperPose is a freely available web server designed to perform both pairwise and multiple protein structure superpositions. The “Structural superposition” term refers to the rotations and translations performed on one structure to make it match or align with another structure or structures. Structural superposition can be quantified either in terms of similarity or difference measures. The optimal superposition is the one in which the similarity measure is maximized or the difference measure is minimized. The “SuperPose” web server uses “RMSD” or Root-Mean-Square Deviation as a difference measure to find the optimal pairwise or multiple protein structure superposition. After an initial sequence and secondary structure alignment, SuperPose generates a Difference Distance (DD) matrix from the equivalent C-alpha atoms of two molecules. The sequence/structure alignment and DD matrix analysis information is then fed into a modified quaternion eigenvalue algorithm to rapidly perform the structural superposition and calculate the RMSD between aligned regions of two macromolecules.













