Rothalpy (or trothalpy) , a short name of rotational stagnation enthalpy, is a fluid mechanical property of importance in the study of flow within rotating systems. [1]
Rothalpy (or trothalpy) , a short name of rotational stagnation enthalpy, is a fluid mechanical property of importance in the study of flow within rotating systems. [1]
Consider we have an inertial frame of reference and a rotating frame of reference which both are sharing common origin . Assume that frame is rotating around a fixed axis with angular velocity . Now assuming fluid velocity to be and fluid velocity relative to rotating frame of reference to be :
Rothalpy of a fluid point can be defined as
where and and is the stagnation enthalpy of fluid point relative to the rotating frame of reference , which is given by
and is known as relative stagnation enthalpy.
Rothalpy can also be defined in terms of absolute stagnation enthalpy:
where is tangential component of fluid velocity . [1] [2] [3] [4]
Rothalpy has applications in turbomachinery and study of relative flows in rotating systems.
One such application is that for steady, adiabatic and irreversible flow in a turbomachine, the value of rothalpy across a blade remains constant along a flow streamline:
so Euler equation of turbomachinery can be written in terms of rothalpy.
This form of the Euler work equation shows that, for rotating blade rows, the relative stagnation enthalpy is constant through the blades provided the blade speed is constant. In other words, , if the radius of a streamline passing through the blades stays the same. This result is important for analyzing turbomachinery flows in the relative frame of reference. [2]
The function was first introduced by Wu (1952) and has acquired the widely used name rothalpy. [2]
This quantity is commonly called rothalpy, a compound word combining the terms rotation and enthalpy. However, its construction does not conform to the established rules for formation of new words in the English language, namely, that the roots of the new word originate from the same language. The word trothalpy satisfies this requirement as trohos is the Greek root for wheel and enthalpy is to put heat in, whereas rotation is derived from Latin rotare. [3]

In physics, angular momentum is the rotational analog of linear momentum. It is an important quantity in physics because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Motorcycles, frisbees and rifled bullets all owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes have spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system but does not uniquely determine it.

In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.

In physics, the Navier–Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In physics, angular velocity or rotational velocity, also known as angular frequency vector, is a vector measure of rotation rate, that refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time.
In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point, as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings.

Centrifugal compressors, sometimes called radial compressors, are a sub-class of dynamic axisymmetric work-absorbing turbomachinery.

In fluid dynamics, the Euler equations are a set of quasilinear hyperbolic equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. The equations represent Cauchy equations of conservation of mass (continuity), and balance of momentum and energy, and can be seen as particular Navier–Stokes equations with zero viscosity and zero thermal conductivity. In fact, Euler equations can be obtained by linearization of some more precise continuity equations like Navier–Stokes equations in a local equilibrium state given by a Maxwellian. The Euler equations can be applied to incompressible and to compressible flow – assuming the flow velocity is a solenoidal field, or using another appropriate energy equation respectively. Historically, only the incompressible equations have been derived by Euler. However, fluid dynamics literature often refers to the full set – including the energy equation – of the more general compressible equations together as "the Euler equations".
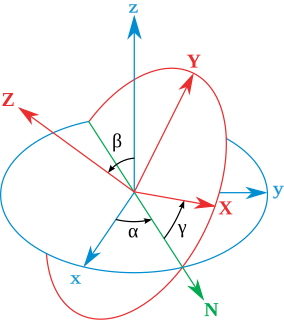
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.
In classical mechanics, Euler's rotation equations are a vectorial quasilinear first-order ordinary differential equation describing the rotation of a rigid body, using a rotating reference frame with its axes fixed to the body and parallel to the body's principal axes of inertia. Their general form is:
In fluid dynamics, helicity is, under appropriate conditions, an invariant of the Euler equations of fluid flow, having a topological interpretation as a measure of linkage and/or knottedness of vortex lines in the flow. This was first proved by Jean-Jacques Moreau in 1961 and Moffatt derived it in 1969 without the knowledge of Moreau's paper. This helicity invariant is an extension of Woltjer's theorem for magnetic helicity.

A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth.

An axial compressor is a gas compressor that can continuously pressurize gases. It is a rotating, airfoil-based compressor in which the gas or working fluid principally flows parallel to the axis of rotation, or axially. This differs from other rotating compressors such as centrifugal compressor, axi-centrifugal compressors and mixed-flow compressors where the fluid flow will include a "radial component" through the compressor. The energy level of the fluid increases as it flows through the compressor due to the action of the rotor blades which exert a torque on the fluid. The stationary blades slow the fluid, converting the circumferential component of flow into pressure. Compressors are typically driven by an electric motor or a steam or a gas turbine.

Stokes flow, also named creeping flow or creeping motion, is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. . This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature this type of flow occurs in the swimming of microorganisms, sperm and the flow of lava. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.

A radial turbine is a turbine in which the flow of the working fluid is radial to the shaft. The difference between axial and radial turbines consists in the way the fluid flows through the components. Whereas for an axial turbine the rotor is 'impacted' by the fluid flow, for a radial turbine, the flow is smoothly orientated perpendicular to the rotation axis, and it drives the turbine in the same way water drives a watermill. The result is less mechanical stress which enables a radial turbine to be simpler, more robust, and more efficient when compared to axial turbines. When it comes to high power ranges the radial turbine is no longer competitive and the efficiency becomes similar to that of the axial turbines.
Crocco's theorem is an aerodynamic theorem relating the flow velocity, vorticity, and stagnation pressure of a potential flow. Crocco's theorem gives the relation between the thermodynamics and fluid kinematics. The theorem was first enunciated by Alexander Friedmann for the particular case of a perfect gas and published in 1922:
In turbomachinery, Degree of reaction or reaction ratio (R) is defined as the ratio of the static pressure drop in the rotor to the static pressure drop in the stage or as the ratio of static enthalpy drop in the rotor to the static enthalpy drop in the stage.
Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.
In turbomachinery, the slip factor is a measure of the fluid slip in the impeller of a compressor or a turbine, mostly a centrifugal machine. Fluid slip is the deviation in the angle at which the fluid leaves the impeller from the impeller's blade/vane angle. Being quite small in axial impellers(inlet and outlet flow in the same direction), slip is a very important phenomenon in radial impellers and is useful in determining the accurate estimation of work input or the energy transfer between the impeller and the fluid, rise in pressure and the velocity triangles at the impeller exit.