In mathematics, the geometric algebra (GA) of a vector space is an algebra over a field, noted for its multiplication operation called the geometric product on a space of elements called multivectors, which contains both the scalars and the vector space .

In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360°. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors.

In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry, theoretical physics and digital image processing. They are named after the English mathematician William Kingdon Clifford.
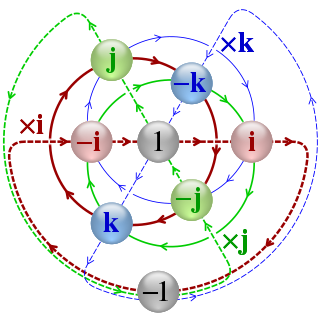
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.
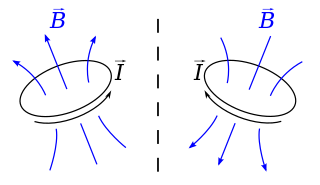
In physics and mathematics, a pseudovector is a quantity that is defined as a function of some vectors or other geometric shapes, that resembles a vector, and behaves like a vector in many situations, but is changed into its opposite if the orientation of the space is changed, or an improper rigid transformation such as a reflection is applied to the whole figure. Geometrically, the direction of a reflected pseudovector is opposite to its mirror image, but with equal magnitude. In contrast, the reflection of a true vector is exactly the same as its mirror image.
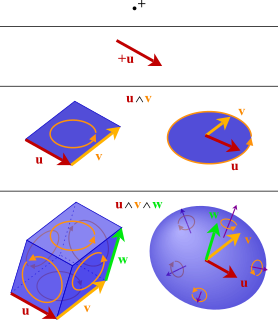
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors and , denoted by , is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of can be interpreted as the area of the parallelogram with sides and , which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning that for all vectors and , but, unlike the cross product, the exterior product is associative.
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebras.

William Kingdon Clifford was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour. The operations of geometric algebra have the effect of mirroring, rotating, translating, and mapping the geometric objects that are being modelled to new positions. Clifford algebras in general and geometric algebra in particular have been of ever increasing importance to mathematical physics, geometry, and computing. Clifford was the first to suggest that gravitation might be a manifestation of an underlying geometry. In his philosophical writings he coined the expression mind-stuff.
![Spin group Lie group in theoretical physics, predicting properties of [[spin (physics)|spin]]](https://upload.wikimedia.org/wikipedia/commons/thumb/5/5f/Cyclic_group.svg/320px-Cyclic_group.svg.png)
In mathematics the spin group Spin(n) is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups

David Orlin Hestenes is a theoretical physicist and science educator. He is best known as chief architect of geometric algebra as a unified language for mathematics and physics, and as founder of Modelling Instruction, a research-based program to reform K–12 Science, Technology, Engineering, and Mathematics (STEM) education.
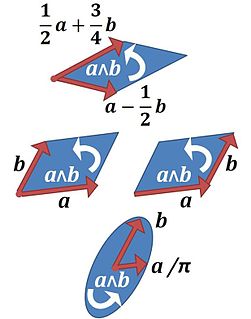
In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. If a scalar is considered a degree zero quantity, and a vector is a degree one quantity, then a bivector can be thought of as being of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex numbers in two dimensions and to both pseudovectors and quaternions in three dimensions. They can be used to generate rotations in any number of dimensions, and are a useful tool for classifying such rotations. They are also used in physics, tying together a number of otherwise unrelated quantities.
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group.
In physics, the algebra of physical space (APS) is the use of the Clifford or geometric algebra Cl3,0(R) of the three-dimensional Euclidean space as a model for (3+1)-dimensional spacetime, representing a point in spacetime via a paravector.
In multilinear algebra, a multivector, sometimes called Clifford number, is an element of the exterior algebra Λ(V) of a vector space V. This algebra is graded, associative and alternating, and consists of linear combinations of simplek-vectors of the form
In mathematical physics, spacetime algebra (STA) is a name for the Clifford algebra Cl1,3(R), or equivalently the geometric algebra G(M4). According to David Hestenes, spacetime algebra can be particularly closely associated with the geometry of special relativity and relativistic spacetime.
In the study of geometric algebras, a k-blade or a simple k-vector is a generalization of the concept of scalars and vectors to include simple bivectors, trivectors, etc. Specifically, a k-blade is a k-vector that can be expressed as the exterior product of 1-vectors, and is of gradek.
In geometry, a plane of rotation is an abstract object used to describe or visualize rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.
Conformal geometric algebra (CGA) is the geometric algebra constructed over the resultant space of a map from points in an n-dimensional base space ℝp,q to null vectors in ℝp+1,q+1. This allows operations on the base space, including reflections, rotations and translations to be represented using versors of the geometric algebra; and it is found that points, lines, planes, circles and spheres gain particularly natural and computationally amenable representations.
In mathematics, a universal geometric algebra is a type of geometric algebra generated by real vector spaces endowed with an indefinite quadratic form. Some authors restrict this to the infinite-dimensional case.
In geometric algebra, the outermorphism of a linear function between vector spaces is a natural extension of the map to arbitrary multivectors. It is the unique unital algebra homomorphism of exterior algebras whose restriction to the vector spaces is the original function.























![Spin group Lie group in theoretical physics, predicting properties of [[spin (physics)|spin]]](https://upload.wikimedia.org/wikipedia/commons/thumb/5/5f/Cyclic_group.svg/320px-Cyclic_group.svg.png)


