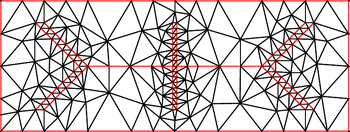
In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with history stretching back to antiquity.

In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane. For each seed there is a corresponding region consisting of all points of the plane closer to that seed than to any other. These regions are called Voronoi cells. The Voronoi diagram of a set of points is dual to its Delaunay triangulation.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".

The Euclidean minimum spanning tree or EMST is a minimum spanning tree of a set of n points in the plane, where the weight of the edge between each pair of points is the Euclidean distance between those two points. In simpler terms, an EMST connects a set of dots using lines such that the total length of all the lines is minimized and any dot can be reached from any other by following the lines.
In geometry, a triangulation is a subdivision of a planar object into triangles, and by extension the subdivision of a higher-dimension geometric object into simplices. Triangulations of a three-dimensional volume would involve subdividing it into tetrahedra packed together.

In computer science and electrical engineering, Lloyd's algorithm, also known as Voronoi iteration or relaxation, is an algorithm named after Stuart P. Lloyd for finding evenly spaced sets of points in subsets of Euclidean spaces and partitions of these subsets into well-shaped and uniformly sized convex cells. Like the closely related k-means clustering algorithm, it repeatedly finds the centroid of each set in the partition and then re-partitions the input according to which of these centroids is closest. In this setting, the mean operation is an integral over a region of space, and the nearest centroid operation results in Voronoi diagrams.

A triangulated irregular network (TIN) is a representation of a continuous surface consisting entirely of triangular facets, used mainly as Discrete Global Grid in primary elevation modeling.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. The goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.
In computational geometry, the Bowyer–Watson algorithm is a method for computing the Delaunay triangulation of a finite set of points in any number of dimensions. The algorithm can be also used to obtain a Voronoi diagram of the points, which is the dual graph of the Delaunay triangulation.
Parallel mesh generation in numerical analysis is a new research area between the boundaries of two scientific computing disciplines: computational geometry and parallel computing. Parallel mesh generation methods decompose the original mesh generation problem into smaller subproblems which are solved (meshed) in parallel using multiple processors or threads. The existing parallel mesh generation methods can be classified in terms of two basic attributes:
- the sequential technique used for meshing the individual subproblems and
- the degree of coupling between the subproblems.

In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points p and q by an edge whenever there does not exist a third point r that is closer to both p and q than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.
The J. H. Wilkinson Prize for Numerical Software is awarded every four years to honor outstanding contributions in the field of numerical software. The award is named to commemorate the outstanding contributions of James H. Wilkinson in the same field.
Jump-and-Walk is an algorithm for point location in triangulations. Surprisingly, the algorithm does not need any preprocessing or complex data structures except some simple representation of the triangulation itself. The predecessor of Jump-and-Walk was due to Lawson (1977) and Green and Sibson (1978), which picks a random starting point S and then walks from S toward the query point Q one triangle at a time. But no theoretical analysis was known for these predecessors until after mid-1990s.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.

In computational geometry, the Urquhart graph of a set of points in the plane, named after Roderick B. Urquhart, is obtained by removing the longest edge from each triangle in the Delaunay triangulation.
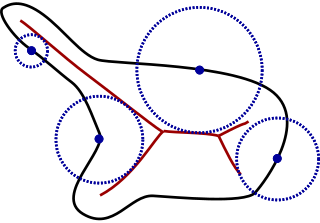
Local feature size refers to several related concepts in computer graphics and computational geometry for measuring the size of a geometric object near a particular point.

In mesh generation, Chew's second algorithm is a Delaunay refinement algorithm for creating quality constrained Delaunay triangulations. The algorithm takes a piecewise linear system (PLS) and returns a constrained Delaunay triangulation of only quality triangles where quality is defined by the minimum angle in a triangle. Developed by L. Paul Chew for meshing surfaces embedded in three-dimensional space, Chew's second algorithm has been adopted as a two-dimensional mesh generator due to practical advantages over Ruppert's algorithm in certain cases and is the default quality mesh generator implemented in the freely available Triangle package. Chew's second algorithm is guaranteed to terminate and produce a local feature size-graded meshes with minimum angle up to about 28.6 degrees.
In computational geometry, a constrained Delaunay triangulation is a generalization of the Delaunay triangulation that forces certain required segments into the triangulation. Because a Delaunay triangulation is almost always unique, often a constrained Delaunay triangulation contains edges that do not satisfy the Delaunay condition. Thus a constrained Delaunay triangulation often is not a Delaunay triangulation itself.

In computational geometry, the farthest-first traversal of a bounded metric space is a sequence of points in the space, where the first point is selected arbitrarily and each successive point is as far as possible from the set of previously-selected points. The same concept can also be applied to a finite set of geometric points, by restricting the selected points to belong to the set or equivalently by considering the finite metric space generated by these points. For a finite metric space or finite set of geometric points, the resulting sequence forms a permutation of the points, known as the greedy permutation.