Scheduling (production processes)

Last updated March 18, 2024

Scheduling is the process of arranging, controlling and optimizing work and workloads in a production process or manufacturing process. Scheduling is used to allocate plant and machinery resources, plan human resources, plan production processes and purchase materials.

It is an important tool for manufacturing and engineering, where it can have a major impact on the productivity of a process. In manufacturing, the purpose of scheduling is to keep due dates of customers and then minimize the production time and costs, by telling a production facility when to make, with which staff, and on which equipment. Production scheduling aims to maximize the efficiency of the operation, utilize maximum resources available and reduce costs.

In some situations, scheduling can involve random attributes, such as random processing times, random due dates, random weights, and stochastic machine breakdowns. In this case, the scheduling problems are referred to as "stochastic scheduling".

Overview

Scheduling is the process of arranging, controlling and optimizing work and workloads in a production process. Companies use backward and forward scheduling to allocate plant and machinery resources, plan human resources, plan production processes and purchase materials.

Forward scheduling is planning the tasks from the date resources become available to determine the shipping date or the due date.
Backward scheduling is planning the tasks from the due date or required-by date to determine the start date and/or any changes in capacity required.

The benefits of production scheduling include:

Process change-over reduction
Inventory reduction, levelling
Reduced scheduling effort
Increased production efficiency
Labour load levelling
Accurate delivery date quotes
Real time information
Accurately measure utilized man/equipment hours

Production scheduling tools greatly outperform older manual scheduling methods. These provide the production scheduler with powerful graphical interfaces which can be used to visually optimize real-time work loads in various stages of production, and pattern recognition allows the software to automatically create scheduling opportunities which might not be apparent without this view into the data. For example, an airline might wish to minimize the number of airport gates required for its aircraft, in order to reduce costs, and scheduling software can allow the planners to see how this can be done, by analysing time tables, aircraft usage, or the flow of passengers.

Key concepts in scheduling

A key character of scheduling is the productivity, the relation between quantity of inputs and quantity of output. Key concepts here are:

Inputs : Inputs are plant, labour, materials, tooling, energy and a clean environment.
Outputs : Outputs are the products produced in factories either for other factories or for the end buyer. The extent to which any one product is produced within any one factory is governed by transaction cost.
Output within the factory : The output of any one work area within the factory is an input to the next work area in that factory according to the manufacturing process. For example, the output of cutting is an input to the bending room.
Output for the next factory : By way of example, the output of a paper mill is an input to a print factory. The output of a petrochemicals plant is an input to an asphalt plant, a cosmetics factory and a plastics factory.
Output for the end buyer : Factory output goes to the consumer via a service business such as a retailer or an asphalt paving company.
Resource allocation : Resource allocation is assigning inputs to produce output. The aim is to maximize output with given inputs or to minimize quantity of inputs to produce required output.

Scheduling algorithms

Production scheduling can take a significant amount of computing power if there are a large number of tasks. Therefore, a range of short-cut algorithms (heuristics) (a.k.a. dispatching rules) are used:

Stochastic Algorithms : Economic Lot Scheduling Problem and Economic production quantity
Heuristic Algorithms : Modified due date scheduling heuristic and Shifting bottleneck heuristic

Batch production scheduling

Batch production scheduling is the practice of planning and scheduling of batch manufacturing processes. Although scheduling may apply to traditionally continuous processes such as refining,^[1]^[2] it is especially important for batch processes such as those for pharmaceutical active ingredients, biotechnology processes and many specialty chemical processes.^[3]^[4] Batch production scheduling shares some concepts and techniques with finite capacity scheduling which has been applied to many manufacturing problems.^[5]

Related Research Articles

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.

An industrial process control or simply process control in continuous production processes is a discipline that uses industrial control systems and control theory to achieve a production level of consistency, economy and safety which could not be achieved purely by human manual control. It is implemented widely in industries such as automotive, mining, dredging, oil refining, pulp and paper manufacturing, chemical processing and power generating plants.

In computer science and mathematical optimization, a metaheuristic is a higher-level procedure or heuristic designed to find, generate, tune, or select a heuristic that may provide a sufficiently good solution to an optimization problem or a machine learning problem, especially with incomplete or imperfect information or limited computation capacity. Metaheuristics sample a subset of solutions which is otherwise too large to be completely enumerated or otherwise explored. Metaheuristics may make relatively few assumptions about the optimization problem being solved and so may be usable for a variety of problems.

Methods engineering is a subspecialty of industrial engineering and manufacturing engineering concerned with human integration in industrial production processes.

A chemical plant is an industrial process plant that manufactures chemicals, usually on a large scale. The general objective of a chemical plant is to create new material wealth via the chemical or biological transformation and or separation of materials. Chemical plants use specialized equipment, units, and technology in the manufacturing process. Other kinds of plants, such as polymer, pharmaceutical, food, and some beverage production facilities, power plants, oil refineries or other refineries, natural gas processing and biochemical plants, water and wastewater treatment, and pollution control equipment use many technologies that have similarities to chemical plant technology such as fluid systems and chemical reactor systems. Some would consider an oil refinery or a pharmaceutical or polymer manufacturer to be effectively a chemical plant.

In computer science and operations research, Genetic fuzzy systems are fuzzy systems constructed by using genetic algorithms or genetic programming, which mimic the process of natural evolution, to identify its structure and parameter.

<span class="mw-page-title-main">Operations management</span> In business operations, controlling the process of production of goods

Operations management is concerned with designing and controlling the production of goods and services, ensuring that businesses are efficient in using resources to meet customer requirements.

In computer science, the min-conflicts algorithm is a search algorithm or heuristic method to solve constraint satisfaction problems.

The ESPRESSO logic minimizer is a computer program using heuristic and specific algorithms for efficiently reducing the complexity of digital logic gate circuits. ESPRESSO-I was originally developed at IBM by Robert K. Brayton et al. in 1982. and improved as ESPRESSO-II in 1984. Richard L. Rudell later published the variant ESPRESSO-MV in 1986 and ESPRESSO-EXACT in 1987. Espresso has inspired many derivatives.

The genetic algorithm is an operational research method that may be used to solve scheduling problems in production planning.

A master production schedule (MPS) is a plan for individual commodities to be produced in each time period such as production, staffing, inventory, etc. It is usually linked to manufacturing where the plan indicates when and how much of each product will be demanded. This plan quantifies significant processes, parts, and other resources in order to optimize production, to identify bottlenecks, and to anticipate needs and completed goods. Since a MPS drives much factory activity, its accuracy and viability dramatically affect profitability. Typical MPSs are created by software with user tweaking.

Manufacturing execution systems (MES) are computerized systems used in manufacturing to track and document the transformation of raw materials to finished goods. MES provides information that helps manufacturing decision-makers understand how current conditions on the plant floor can be optimized to improve production output. MES works as real-time monitoring system to enable the control of multiple elements of the production process.

Demand Flow Technology (DFT) is a strategy for defining and deploying business processes in a flow, driven in response to customer demand. DFT is based on a set of applied mathematical tools that are used to connect processes in a flow and link it to daily changes in demand. DFT represents a scientific approach to flow manufacturing for discrete production. It is built on principles of demand pull where customer demand is the central signal to guide factory and office activity in the daily operation. DFT is intended to provide an alternative to schedule-push manufacturing which primarily uses a sales plan and forecast to determine a production schedule.

Material theory is the sub-specialty within operations research and operations management that is concerned with the design of production/inventory systems to minimize costs: it studies the decisions faced by firms and the military in connection with manufacturing, warehousing, supply chains, spare part allocation and so on and provides the mathematical foundation for logistics. The inventory control problem is the problem faced by a firm that must decide how much to order in each time period to meet demand for its products. The problem can be modeled using mathematical techniques of optimal control, dynamic programming and network optimization. The study of such models is part of inventory theory.

Industrial engineering is an engineering profession that is concerned with the optimization of complex processes, systems, or organizations by developing, improving and implementing integrated systems of people, money, knowledge, information and equipment. Industrial engineering is central to manufacturing operations.

Plant Simulation is a computer application developed by Siemens Digital Industries Software for modelling, simulating, analyzing, visualizing and optimizing production systems and processes, the flow of materials and logistic operations. Plant Simulation, allows users to optimize material flow and resource utilization and logistics for all levels of plant planning from global production facilities, through local plants, to specific lines. Within the Plant Design and Optimization Solution, the software portfolio, to which Plant Simulation belongs, is — together with the products of the Digital Factory and of Digital Manufacturing — part of the Product Lifecycle Management Software (PLM). The application allows comparing complex production alternatives, including the immanent process logic, by means of computer simulations. Plant Simulation is used by individual production planners as well as by multi-national enterprises, primarily to strategically plan layout, and control logic and dimensions of large, complex production investments. It is one of the major products that dominate that market space.

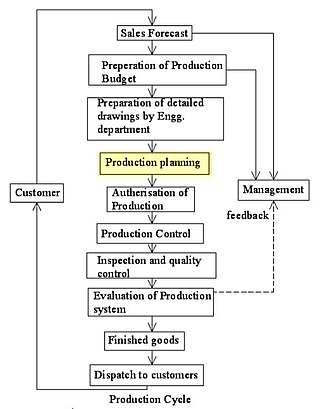
Production planning is the planning of production and manufacturing modules in a company or industry. It utilizes the resource allocation of activities of employees, materials and production capacity, in order to serve different customers.

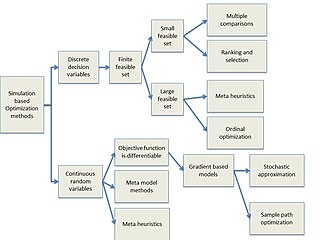
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques.

Stochastic scheduling concerns scheduling problems involving random attributes, such as random processing times, random due dates, random weights, and stochastic machine breakdowns. Major applications arise in manufacturing systems, computer systems, communication systems, logistics and transportation, and machine learning, among others.

References

↑ Marcus V. Magalhaes and Nilay Shah, “Crude Oil Scheduling,” Foundations of Computer-Aided Operations (FOCAPO) 2003, pp 323-325.
↑ Zhenya Jia and Marianthi Ierapetritou, “Efficient Short-Term Scheduling of Refinery Operation Based on a Continuous Time Formulation,” Foundations of Computer-Aided Operations (FOCAPO) 2003, pp 327-330
↑ Toumi, A., Jurgens, C., Jungo, C., MAier, B.A., Papavasileiou, V., and Petrides, D., “Design and Optimization of a Large Scale Biopharmaceutical Facility using Process Simulation and Scheduling Tools,” Pharmaceutical Engineering (the ISPE magazine) 2010, vol 30, no 2, pp 1-9.
↑ Papavasileiou, V., Koulouris, A., Siletti, C., and Petrides, D., “Optimize Manufacturing of Pharmaceutical Products with Process Simulation and Production Scheduling Tools,” Chemical Engineering Research and Design (IChemE publication) 2007, vol 87, pp 1086-1097
↑ Michael Pinedo, Scheduling Theory, Algorithms, and Systems, Prentice Hall, 2002, pp 1-6.