
Dots and boxes is a pencil-and-paper game for two players. It was first published in the 19th century by French mathematician Édouard Lucas, who called it la pipopipette. It has gone by many other names, including dots and dashes, game of dots, dot to dot grid, boxes, and pigs in a pen.
In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
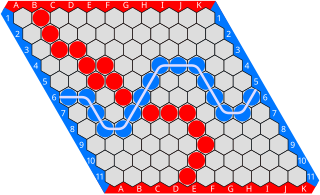
Hex is a two player abstract strategy board game in which players attempt to connect opposite sides of a rhombus-shaped board made of hexagonal cells. Hex was invented by mathematician and poet Piet Hein in 1942 and later rediscovered and popularized by John Nash.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

TwixT is a two-player strategy board game, an early entrant in the 1960s 3M bookshelf game series. It became one of the most popular and enduring games in the series. It is a connection game where players alternate turns placing pegs and links on a pegboard in an attempt to link their opposite sides. While TwixT itself is simple, the game also requires strategy, so young children can play it, but it also appeals to adults. The game has been discontinued except in Germany and Japan.
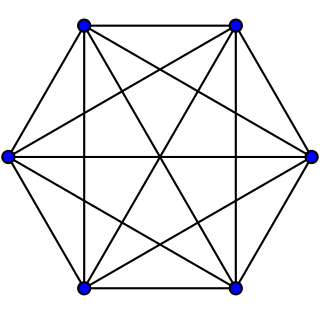
Sim is a two-player paper-and-pencil game.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
The Black Path Game is a two-player board game described and analysed in Winning Ways for your Mathematical Plays. It was invented by Larry Black in 1960.
In the mathematical field of graph theory, Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff is a theorem about the number of spanning trees in a graph, showing that this number can be computed in polynomial time from the determinant of a submatrix of the Laplacian matrix of the graph; specifically, the number is equal to any cofactor of the Laplacian matrix. Kirchhoff's theorem is a generalization of Cayley's formula which provides the number of spanning trees in a complete graph.

In the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n – 1)-gonal pyramid. Some authors write Wn to denote a wheel graph with n vertices ; other authors instead use Wn to denote a wheel graph with n + 1 vertices, which is formed by connecting a single vertex to all vertices of a cycle of length n. The rest of this article uses the former notation.
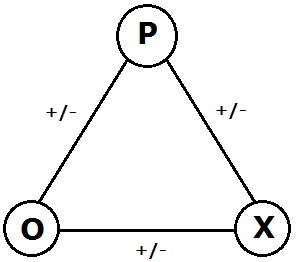
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph. The Nash-Williams theorem provides necessary and sufficient conditions for when a graph is k-arboric.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.

In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees equals twice the number of edges in the graph. Both results were proven by Leonhard Euler in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
In the mathematical subject of matroid theory, the bicircular matroid of a graph G is the matroid B(G) whose points are the edges of G and whose independent sets are the edge sets of pseudoforests of G, that is, the edge sets in which each connected component contains at most one cycle.
A connection game is a type of abstract strategy game in which players attempt to complete a specific type of connection with their pieces. This could involve forming a path between two or more endpoints, completing a closed loop, or connecting all of one's pieces so they are adjacent to each other. Connection games typically have simple rules, but complex strategies. They have minimal components and may be played as board games, computer games, or even paper-and-pencil games.

In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.














