In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, for which only integer solutions are of interest. A linear Diophantine equation equates to a constant the sum of two or more monomials, each of degree one. An exponential Diophantine equation is one in which unknowns can appear in exponents.

Enrico Bombieri is an Italian mathematician, known for his work in analytic number theory, Diophantine geometry, complex analysis, and group theory. Bombieri is currently professor emeritus in the School of Mathematics at the Institute for Advanced Study in Princeton, New Jersey. Bombieri won the Fields Medal in 1974 for his work on the large sieve and its application to the distribution of prime numbers.
In mathematics, a transcendental number is a real or complex number that is not algebraic: that is, not the root of a non-zero polynomial with integer coefficients. The best-known transcendental numbers are π and e. The quality of a number being transcendental is called transcendence.
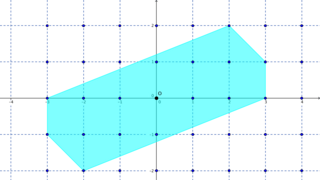
In mathematics, Minkowski's theorem is the statement that every convex set in which is symmetric with respect to the origin and which has volume greater than contains a non-zero integer point. The theorem was proved by Hermann Minkowski in 1889 and became the foundation of the branch of number theory called the geometry of numbers. It can be extended from the integers to any lattice and to any symmetric convex set with volume greater than , where denotes the covolume of the lattice.

Faltings's theorem is a result in arithmetic geometry, according to which a curve of genus greater than 1 over the field of rational numbers has only finitely many rational points. This was conjectured in 1922 by Louis Mordell, and known as the Mordell conjecture until its 1983 proof by Gerd Faltings. The conjecture was later generalized by replacing by any number field.

Geometry of numbers is the part of number theory which uses geometry for the study of algebraic numbers. Typically, a ring of algebraic integers is viewed as a lattice in and the study of these lattices provides fundamental information on algebraic numbers. Hermann Minkowski initiated this line of research at the age of 26 in his work The Geometry of Numbers.

In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria.
In mathematics, Diophantine geometry is the study of Diophantine equations by means of powerful methods in algebraic geometry. By the 20th century it became clear for some mathematicians that methods of algebraic geometry are ideal tools to study these equations. Diophantine geometry is part of the broader field of arithmetic geometry.
In mathematics, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real algebraic integer greater than 1, all of whose Galois conjugates are less than 1 in absolute value. These numbers were discovered by Axel Thue in 1912 and rediscovered by G. H. Hardy in 1919 within the context of Diophantine approximation. They became widely known after the publication of Charles Pisot's dissertation in 1938. They also occur in the uniqueness problem for Fourier series. Tirukkannapuram Vijayaraghavan and Raphael Salem continued their study in the 1940s. Salem numbers are a closely related set of numbers.
In mathematics, Roth's theorem or Thue–Siegel–Roth theorem is a fundamental result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that algebraic numbers cannot have many rational approximations that are 'very good'. Over half a century, the meaning of very good here was refined by a number of mathematicians, starting with Joseph Liouville in 1844 and continuing with work of Axel Thue, Carl Ludwig Siegel, Freeman Dyson, and Klaus Roth.
In mathematics, a Thue equation is a Diophantine equation of the form
Transcendental number theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.
In number theory, Dirichlet's theorem on Diophantine approximation, also called Dirichlet's approximation theorem, states that for any real numbers and , with , there exist integers and such that and
In number theory and algebraic geometry, a rational point of an algebraic variety is a point whose coordinates belong to a given field. If the field is not mentioned, the field of rational numbers is generally understood. If the field is the field of real numbers, a rational point is more commonly called a real point.
This is a glossary of arithmetic and diophantine geometry in mathematics, areas growing out of the traditional study of Diophantine equations to encompass large parts of number theory and algebraic geometry. Much of the theory is in the form of proposed conjectures, which can be related at various levels of generality.
A height function is a function that quantifies the complexity of mathematical objects. In Diophantine geometry, height functions quantify the size of solutions to Diophantine equations and are typically functions from a set of points on algebraic varieties to the real numbers.
In mathematics, Siegel's theorem on integral points states that a curve of genus greater than zero has only finitely many integral points over any given number field.
In mathematics, the subspace theorem says that points of small height in projective space lie in a finite number of hyperplanes. It is a result obtained by Wolfgang M. Schmidt.
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high order at some point.
In transcendental number theory, a mathematical discipline, Baker's theorem gives a lower bound for the absolute value of linear combinations of logarithms of algebraic numbers. Nearly fifteen years earlier, Alexander Gelfond had considered the problem with only integer coefficients to be of "extraordinarily great significance". The result, proved by Alan Baker, subsumed many earlier results in transcendental number theory. Baker used this to prove the transcendence of many numbers, to derive effective bounds for the solutions of some Diophantine equations, and to solve the class number problem of finding all imaginary quadratic fields with class number 1.











