
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
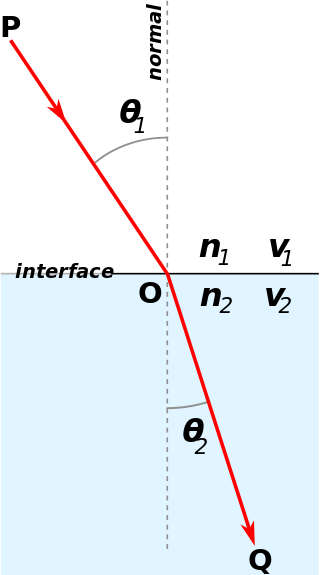
Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index.

The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. It treats a gas as composed of numerous particles, too small to see with a microscope, which are constantly in random motion. Their collisions with each other and with the walls of their container are used to explain physical properties of the gas—for example, the relationship between its temperature, pressure, and volume. The particles are now known to be the atoms or molecules of the gas.

In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.
The Phong reflection model is an empirical model of the local illumination of points on a surface designed by the computer graphics researcher Bui Tuong Phong. In 3D computer graphics, it is sometimes referred to as "Phong shading", particularly if the model is used with the interpolation method of the same name and in the context of pixel shaders or other places where a lighting calculation can be referred to as “shading”.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
In physics, a wave vector is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave, and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation.

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive.

The Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. They can be determined from directly observable phenomena. The original Stokes paper was discovered independently by Francis Perrin in 1942 and by Subrahamanyan Chandrasekhar in 1947, who named it as the Stokes parameters.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
The Blinn–Phong reflection model, also called the modified Phong reflection model, is a modification developed by Jim Blinn to the Phong reflection model.

A pendulum is a body suspended from a fixed support such that it freely swings back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back towards the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.
The direct-quadrature-zerotransformation or zero-direct-quadraturetransformation is a tensor that rotates the reference frame of a three-element vector or a three-by-three element matrix in an effort to simplify analysis. The DQZ transform is the product of the Clarke transform and the Park transform, first proposed in 1929 by Robert H. Park.
Contact mechanics is the study of the deformation of solids that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and frictional forces in the tangential direction. Frictional contact mechanics is the study of the deformation of bodies in the presence of frictional effects, whereas frictionless contact mechanics assumes the absence of such effects.
In optics, polarization mixing refers to changes in the relative strengths of the Stokes parameters caused by reflection or scattering—see vector radiative transfer—or by changes in the radial orientation of the detector.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.

Earth section paths are plane curves defined by the intersection of an earth ellipsoid and a plane. Common examples include the great ellipse and normal sections. Earth section paths are useful as approximate solutions for geodetic problems, the direct and inverse calculation of geographic distances. The rigorous solution of geodetic problems involves skew curves known as geodesics.









































