Diffuse reflection

Last updated
Diffuse and specular reflection from a glossy surface. The rays represent luminous intensity, which varies according to Lambert's cosine law for an ideal diffuse reflector. Lambert2.gif
Diffuse and specular reflection from a glossy surface. The rays represent luminous intensity, which varies according to Lambert's cosine law for an ideal diffuse reflector.

Diffuse reflection is the reflection of light or other waves or particles from a surface such that a ray incident on the surface is scattered at many angles rather than at just one angle as in the case of specular reflection. An ideal diffuse reflecting surface is said to exhibit Lambertian reflection, meaning that there is equal luminance when viewed from all directions lying in the half-space adjacent to the surface.

Contents

A surface built from a non-absorbing powder such as plaster, or from fibers such as paper, or from a polycrystalline material such as white marble, reflects light diffusely with great efficiency. Many common materials exhibit a mixture of specular and diffuse reflection.

The visibility of objects, excluding light-emitting ones, is primarily caused by diffuse reflection of light: it is diffusely-scattered light that forms the image of the object in the observer's eye.

Mechanism

Figure 1 - General mechanism of diffuse reflection by a solid surface (refraction phenomena not represented) Diffuse reflection.gif
Figure 1 – General mechanism of diffuse reflection by a solid surface (refraction phenomena not represented)
Figure 2 - Diffuse reflection from an irregular surface Diffuse reflection.svg
Figure 2 – Diffuse reflection from an irregular surface

Diffuse reflection from solids is generally not due to surface roughness. A flat surface is indeed required to give specular reflection, but it does not prevent diffuse reflection. A piece of highly polished white marble remains white; no amount of polishing will turn it into a mirror. Polishing produces some specular reflection, but the remaining light continues to be diffusely reflected.

The most general mechanism by which a surface gives diffuse reflection does not involve exactly the surface: most of the light is contributed by scattering centers beneath the surface, [2] [3] as illustrated in Figure 1. If one were to imagine that the figure represents snow, and that the polygons are its (transparent) ice crystallites, an impinging ray is partially reflected (a few percent) by the first particle, enters in it, is again reflected by the interface with the second particle, enters in it, impinges on the third, and so on, generating a series of "primary" scattered rays in random directions, which, in turn, through the same mechanism, generate a large number of "secondary" scattered rays, which generate "tertiary" rays, and so forth. [4] All these rays walk through the snow crystallites, which do not absorb light, until they arrive at the surface and exit in random directions. [5] The result is that the light that was sent out is returned in all directions, so that snow is white despite being made of transparent material (ice crystals).

For simplicity, "reflections" are spoken of here, but more generally the interface between the small particles that constitute many materials is irregular on a scale comparable with light wavelength, so diffuse light is generated at each interface, rather than a single reflected ray, but the story can be told the same way.

This mechanism is very general, because almost all common materials are made of "small things" held together. Mineral materials are generally polycrystalline: one can describe them as made of a 3D mosaic of small, irregularly shaped defective crystals. Organic materials are usually composed of fibers or cells, with their membranes and their complex internal structure. And each interface, inhomogeneity or imperfection can deviate, reflect or scatter light, reproducing the above mechanism.

Few materials do not cause diffuse reflection: among these are metals, which do not allow light to enter; gases, liquids, glass, and transparent plastics (which have a liquid-like amorphous microscopic structure); single crystals, such as some gems or a salt crystal; and some very special materials, such as the tissues which make the cornea and the lens of an eye. These materials can reflect diffusely, however, if their surface is microscopically rough, like in a frost glass (Figure 2), or, of course, if their homogeneous structure deteriorates, as in cataracts of the eye lens.

A surface may also exhibit both specular and diffuse reflection, as is the case, for example, of glossy paints as used in home painting, which give also a fraction of specular reflection, while matte paints give almost exclusively diffuse reflection.

Most materials can give some specular reflection, provided that their surface can be polished to eliminate irregularities comparable with the light wavelength (a fraction of a micrometer). Depending on the material and surface roughness, reflection may be mostly specular, mostly diffuse, or anywhere in between. A few materials, like liquids and glasses, lack the internal subdivisions which produce the subsurface scattering mechanism described above, and so give only specular reflection. Among common materials, only polished metals can reflect light specularly with high efficiency, as in aluminum or silver usually used in mirrors. All other common materials, even when perfectly polished, usually give not more than a few percent specular reflection, except in particular cases, such as grazing angle reflection by a lake, or the total reflection of a glass prism, or when structured in certain complex configurations such as the silvery skin of many fish species or the reflective surface of a dielectric mirror. Diffuse reflection can be highly efficient, as in white materials, due to the summing up of the many subsurface reflections.

Colored objects

Up to this point white objects have been discussed, which do not absorb light. But the above scheme continues to be valid in the case that the material is absorbent. In this case, diffused rays will lose some wavelengths during their walk in the material, and will emerge colored.

Diffusion affects the color of objects in a substantial manner because it determines the average path of light in the material, and hence to which extent the various wavelengths are absorbed. [6] Red ink looks black when it stays in its bottle. Its vivid color is only perceived when it is placed on a scattering material (e.g. paper). This is so because light's path through the paper fibers (and through the ink) is only a fraction of millimeter long. However, light from the bottle has crossed several centimeters of ink and has been heavily absorbed, even in its red wavelengths.

And, when a colored object has both diffuse and specular reflection, usually only the diffuse component is colored. A cherry reflects diffusely red light, absorbs all other colors and has a specular reflection which is essentially white (if the incident light is white light). This is quite general, because, except for metals, the reflectivity of most materials depends on their refractive index, which varies little with the wavelength (though it is this variation that causes the chromatic dispersion in a prism), so that all colors are reflected nearly with the same intensity.

Importance for vision

The vast majority of visible objects are seen primarily by diffuse reflection from their surface. [7] [8] Exceptions include objects with polished (specularly reflecting) surfaces, and objects that themselves emit light. Rayleigh scattering is responsible for the blue color of the sky, and Mie scattering for the white color of the water droplets in clouds.

Interreflection

Diffuse interreflection is a process whereby light reflected from an object strikes other objects in the surrounding area, illuminating them. Diffuse interreflection specifically describes light reflected from objects which are not shiny or specular. In real life terms what this means is that light is reflected off non-shiny surfaces such as the ground, walls, or fabric, to reach areas not directly in view of a light source. If the diffuse surface is colored, the reflected light is also colored, resulting in similar coloration of surrounding objects.

In 3D computer graphics, diffuse interreflection is an important component of global illumination. There are a number of ways to model diffuse interreflection when rendering a scene. Radiosity and photon mapping are two commonly used methods.

Spectroscopy

Diffuse reflectance spectroscopy can be used to determine the absorption spectra of powdered samples in cases where transmission spectroscopy is not feasible. This applies to UV-Vis-NIR spectroscopy or mid-infrared spectroscopy. [9] [10]

See also

Related Research Articles

In physics, attenuation or, in some contexts, extinction is the gradual loss of flux intensity through a medium. For instance, dark glasses attenuate sunlight, lead attenuates X-rays, and water and air attenuate both light and sound at variable attenuation rates.

Brewsters angle angle of incidence for which all reflected light will be polarized

Brewster's angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly polarized. This special angle of incidence is named after the Scottish physicist Sir David Brewster (1781–1868).

Reflectance Capacity of an object to reflect light

The reflectance of the surface of a material is its effectiveness in reflecting radiant energy. It is the fraction of incident electromagnetic power that is reflected at the boundary. Reflectance is a component of the response of the electronic structure of the material to the electromagnetic field of light, and is in general a function of the frequency, or wavelength, of the light, its polarization, and the angle of incidence. The dependence of reflectance on the wavelength is called a reflectance spectrum or spectral reflectance curve.

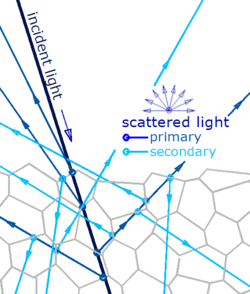
Scattering Range of physical processes

Scattering is a term used in physics to describe a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called diffuse reflections and unscattered reflections are called specular (mirror-like) reflections. Originally, the term was confined to light scattering. As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" in 1800. John Tyndall, a pioneer in light scattering research, noted the connection between light scattering and acoustic scattering in the 1870s. Near the end of the 19th century, the scattering of cathode rays and X-rays was observed and discussed. With the discovery of subatomic particles and the development of quantum theory in the 20th century, the sense of the term became broader as it was recognized that the same mathematical frameworks used in light scattering could be applied to many other phenomena.

In computer graphics, photon mapping is a two-pass global illumination rendering algorithm developed by Henrik Wann Jensen between 1995 and 2001 that approximately solves the rendering equation for integrating light radiance at a given point in space. Rays from the light source and rays from the camera are traced independently until some termination criterion is met, then they are connected in a second step to produce a radiance value. The algorithm is used to realistically simulate the interaction of light with different types of objects. Specifically, it is capable of simulating the refraction of light through a transparent substance such as glass or water, diffuse interreflection between illuminated objects, the subsurface scattering of light in translucent materials, and some of the effects caused by particulate matter such as smoke or water vapor. Photon mapping can also be extended to more accurate simulations of light, such as spectral rendering. Progressive photon mapping (PPM) starts with ray tracing and then adds more and more photon mapping passes to provide a progressively more accurate render.

Transparency and translucency Property of an object or substance to transmit light with minimal scattering

In the field of optics, transparency is the physical property of allowing light to pass through the material without appreciable scattering of light. On a macroscopic scale, the photons can be said to follow Snell's Law. Translucency allows light to pass through, but does not necessarily follow Snell's law; the photons can be scattered at either of the two interfaces, or internally, where there is a change in index of refraction. In other words, a translucent material is made up of components with different indices of refraction. A transparent material is made up of components with a uniform index of refraction. Transparent materials appear clear, with the overall appearance of one color, or any combination leading up to a brilliant spectrum of every color. The opposite property of translucency is opacity.

Reflection (physics) Change in direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated

Reflection is the change in direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves. The law of reflection says that for specular reflection the angle at which the wave is incident on the surface equals the angle at which it is reflected. Mirrors exhibit specular reflection.

Specular reflection Mirror-like wave reflection

Specular reflection, or regular reflection, is the mirror-like reflection of waves, such as light, from a surface.

Backscatter

In physics, backscatter is the reflection of waves, particles, or signals back to the direction from which they came. It is usually a diffuse reflection due to scattering, as opposed to specular reflection as from a mirror, although specular backscattering can occur at normal incidence with a surface. Backscattering has important applications in astronomy, photography, and medical ultrasonography. The opposite effect is forward scatter, e.g. when a translucent material like a cloud diffuses sunlight, giving soft light.

Absorption (electromagnetic radiation) Physical process by which matter takes up a photons energy and stores it

In physics, absorption of electromagnetic radiation is how matter takes up a photon's energy — and so transforms electromagnetic energy into internal energy of the absorber. A notable effect is attenuation, or the gradual reduction of the intensity of light waves as they propagate through a medium. Although the absorption of waves does not usually depend on their intensity, in certain conditions (optics) the medium's transparency changes by a factor that varies as a function of wave intensity, and saturable absorption occurs.

Subsurface scattering

Subsurface scattering (SSS), also known as subsurface light transport (SSLT), is a mechanism of light transport in which light that penetrates the surface of a translucent object is scattered by interacting with the material and exits the surface at a different point. The light will generally penetrate the surface and be reflected a number of times at irregular angles inside the material before passing back out of the material at a different angle than it would have had if it had been reflected directly off the surface. Subsurface scattering is important for realistic 3D computer graphics, being necessary for the rendering of materials such as marble, skin, leaves, wax and milk. If subsurface scattering is not implemented, the material may look unnatural, like plastic or metal.

Bidirectional reflectance distribution function Function of four real variables that defines how light is reflected at an opaque surface

The bidirectional reflectance distribution function is a function of four real variables that defines how light is reflected at an opaque surface. It is employed in the optics of real-world light, in computer graphics algorithms, and in computer vision algorithms. The function takes an incoming light direction, , and outgoing direction, , and returns the ratio of reflected radiance exiting along to the irradiance incident on the surface from direction . Each direction is itself parameterized by azimuth angle and zenith angle , therefore the BRDF as a whole is a function of 4 variables. The BRDF has units sr−1, with steradians (sr) being a unit of solid angle.

Gloss (optics) Optical property describing the ability of a surface to reflect light in a specular direction

Gloss is an optical property which indicates how well a surface reflects light in a specular (mirror-like) direction. It is one of the important parameters that are used to describe the visual appearance of an object. The factors that affect gloss are the refractive index of the material, the angle of incident light and the surface topography.

Diffuse reflectance spectroscopy, or diffuse reflection spectroscopy, is a subset of absorption spectroscopy. It is sometimes called remission spectroscopy. Remission is the reflection or back-scattering of light by a material, while transmission is the passage of light through a material. The word remission implies a direction of scatter, independent of the scattering process. Remission includes both specular and diffusely back-scattered light. The word reflection often implies a particular physical process, such as specular reflection.

Neutron reflectometry

Neutron reflectometry is a neutron diffraction technique for measuring the structure of thin films, similar to the often complementary techniques of X-ray reflectivity and ellipsometry. The technique provides valuable information over a wide variety of scientific and technological applications including chemical aggregation, polymer and surfactant adsorption, structure of thin film magnetic systems, biological membranes, etc.

Computer graphics lighting is the collection of techniques used to simulate light in computer graphics scenes. While lighting techniques offer flexibility in the level of detail and functionality available, they also operate at different levels of computational demand and complexity. Graphics artists can choose from a variety of light sources, models, shading techniques, and effects to suit the needs of each application.

Integrating sphere

An integrating sphere is an optical component consisting of a hollow spherical cavity with its interior covered with a diffuse white reflective coating, with small holes for entrance and exit ports. Its relevant property is a uniform scattering or diffusing effect. Light rays incident on any point on the inner surface are, by multiple scattering reflections, distributed equally to all other points. The effects of the original direction of light are minimized. An integrating sphere may be thought of as a diffuser which preserves power but destroys spatial information. It is typically used with some light source and a detector for optical power measurement. A similar device is the focusing or Coblentz sphere, which differs in that it has a mirror-like (specular) inner surface rather than a diffuse inner surface.

Diffuse reflectance infrared fourier transform spectroscopy (DRIFTS) is an infrared spectroscopy sampling technique used on powder samples without prior preparation. The sample is added to a sample cup and the data is collected on the bulk sample. The infrared light on a sample is reflected and transmitted at different amounts depending on the bulk properties of the material. Diffuse reflection of the incident light produced by the sample's rough surface reflection in all directions is collected by use of an ellipsoid or paraboloid mirror. Shape, compactness, refractive index, reflectivity and absorption of the particles are all characteristic of the material being analyzed. If the sample is too absorbent, then it can be diluted with a nonabsorbent material such as potassium bromide, potassium chloride, etc. The particle size should be smaller than the wavelength of the incident light in order to minimize Mie scattering, so this would infer that it should be less than 5 µm for mid-infrared spectroscopy. The spectra are plotted in units of log inverse reflectance versus wavenumber. Alternative plots of Kubelka-Munk units can be used, which relate reflectance to concentration using a scaling factor. A reflectance standard is needed in order to quantify the reflectance of the sample because it cannot be determined directly.

There are two different types of haze that can occur in materials:

References

  1. ↑ Scott M. Juds (1988). Photoelectric sensors and controls: selection and application. CRC Press. p. 29. ISBN   978-0-8247-7886-6. Archived from the original on 2018-01-14.
  2. ↑ P.Hanrahan and W.Krueger (1993), Reflection from layered surfaces due to subsurface scattering, in SIGGRAPH ’93 Proceedings, J. T. Kajiya, Ed., vol. 27, pp. 165–174 Archived 2010-07-27 at the Wayback Machine .
  3. ↑ H.W.Jensen et al. (2001), A practical model for subsurface light transport, in 'Proceedings of ACM SIGGRAPH 2001', pp. 511–518 Archived 2010-07-27 at the Wayback Machine
  4. ↑ Only primary and secondary rays are represented in the figure.
  5. ↑ Or, if the object is thin, it can exit from the opposite surface, giving diffuse transmitted light.
  6. ↑ Paul Kubelka, Franz Munk (1931), Ein Beitrag zur Optik der Farbanstriche, Zeits. f. Techn. Physik, 12, 593–601, see The Kubelka-Munk Theory of Reflectance Archived 2011-07-17 at the Wayback Machine
  7. ↑ Kerker, M. (1969). The Scattering of Light. New York: Academic.
  8. ↑ Mandelstam, L.I. (1926). "Light Scattering by Inhomogeneous Media". Zh. Russ. Fiz-Khim. Ova. 58: 381.
  9. ↑ Fuller, Michael P.; Griffiths, Peter R. (1978). "Diffuse reflectance measurements by infrared Fourier transform spectrometry". Analytical Chemistry. 50 (13): 1906–1910. doi:10.1021/ac50035a045. ISSN   0003-2700.
  10. ↑ Kortüm, Gustav (1969). Reflectance spectroscopy Principles, methods, applications. Berlin: Springer. ISBN   9783642880711. OCLC   714802320.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.