Luminance

Last updated December 05, 2024

Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction.^[1] It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls within a given solid angle.

Description

Luminance is often used to characterize emission or reflection from flat, diffuse surfaces. Luminance levels indicate how much luminous power could be detected by the human eye looking at a particular surface from a particular angle of view. Luminance is thus an indicator of how bright the surface will appear. In this case, the solid angle of interest is the solid angle subtended by the eye's pupil.

Luminance is used in the video industry to characterize the brightness of displays. A typical computer display emits between 50 and 300 cd/m². The sun has a luminance of about 1.6×10⁹ cd/m² at noon.^[3]

Luminance is invariant in geometric optics.^[4] This means that for an ideal optical system, the luminance at the output is the same as the input luminance.

For real, passive optical systems, the output luminance is at most equal to the input. As an example, if one uses a lens to form an image that is smaller than the source object, the luminous power is concentrated into a smaller area, meaning that the illuminance is higher at the image. The light at the image plane, however, fills a larger solid angle so the luminance comes out to be the same assuming there is no loss at the lens. The image can never be "brighter" than the source.

Health effects

Retinal damage can occur when the eye is exposed to high luminance. Damage can occur because of local heating of the retina. Photochemical effects can also cause damage, especially at short wavelengths.^[5]

The IEC 60825 series gives guidance on safety relating to exposure of the eye to lasers, which are high luminance sources. The IEC 62471 series gives guidance for evaluating the photobiological safety of lamps and lamp systems including luminaires. Specifically it specifies the exposure limits, reference measurement technique and classification scheme for the evaluation and control of photobiological hazards from all electrically powered incoherent broadband sources of optical radiation, including LEDs but excluding lasers, in the wavelength range from 200 nm through 3000 nm. This standard was prepared as Standard CIE S 009:2002 by the International Commission on Illumination.

Luminance meter

A luminance meter is a device used in photometry that can measure the luminance in a particular direction and with a particular solid angle. The simplest devices measure the luminance in a single direction while imaging luminance meters measure luminance in a way similar to the way a digital camera records color images.^[6]

Formulation

Parameters for defining the luminance Etendue.svg — Parameters for defining the luminance

The luminance of a specified point of a light source, in a specified direction, is defined by the mixed partial derivative $L_{\mathrm {v} }={\frac {\mathrm {d} ^{2}\Phi _{\mathrm {v} }}{\mathrm {d} \Sigma \,\mathrm {d} \Omega _{\Sigma }\cos \theta _{\Sigma }}}$ where

$L v$ is the luminance (cd/m²);
$d 2 Φ v$ is the luminous flux (lm) leaving the area $dΣ$ in any direction contained inside the solid angle $dΩ Σ$ ;
$dΣ$ is an infinitesimal area (m²) of the source containing the specified point;
$dΩ Σ$ is an infinitesimal solid angle (sr) containing the specified direction; and
$θ Σ$ is the angle between the normal $n Σ$ to the surface $dΣ$ and the specified direction.^[7]

If light travels through a lossless medium, the luminance does not change along a given light ray. As the ray crosses an arbitrary surface $S$ , the luminance is given by $L_{\mathrm {v} }={\frac {\mathrm {d} ^{2}\Phi _{\mathrm {v} }}{\mathrm {d} S\,\mathrm {d} \Omega _{S}\cos \theta _{S}}}$ where

$d S$ is the infinitesimal area of $S$ seen from the source inside the solid angle $dΩ Σ$ ;
$dΩ S$ is the infinitesimal solid angle subtended by $dΣ$ as seen from $d S$ ; and
$θ S$ is the angle between the normal $n S$ to $d S$ and the direction of the light.

More generally, the luminance along a light ray can be defined as $L_{\mathrm {v} }=n^{2}{\frac {\mathrm {d} \Phi _{\mathrm {v} }}{\mathrm {d} G}}$ where

$d G$ is the etendue of an infinitesimally narrow beam containing the specified ray;
$dΦ v$ is the luminous flux carried by this beam; and
$n$ is the index of refraction of the medium.

Relation to illuminance

The luminance of a reflecting surface is related to the illuminance it receives: $\int _{\Omega _{\Sigma }}L_{\text{v}}\mathrm {d} \Omega _{\Sigma }\cos \theta _{\Sigma }=M_{\text{v}}=E_{\text{v}}R,$ where the integral covers all the directions of emission $Ω Σ$ ,

$M v$ is the surface's luminous exitance;
$E v$ is the received illuminance; and
$R$ is the reflectance.

In the case of a perfectly diffuse reflector (also called a Lambertian reflector), the luminance is isotropic, per Lambert's cosine law. Then the relationship is simply $L_{\text{v}}={\frac {E_{\text{v}}R}{\pi }}.$

Units

A variety of units have been used for luminance, besides the candela per square metre. Luminance is essentially the same as surface brightness, the term used in astronomy. This is measured with a logarithmic scale, magnitudes per square arcsecond (MPSAS).

Units of luminance
v t e		cd/m² (SI unit) ≡ nit ≡ lm/m²/sr	stilb (sb) (CGS unit) ≡ cd/cm²	apostilb (asb) ≡ blondel	bril	skot (sk)	lambert (L)	foot-lambert (fL) = 1 ⁄ $π$ cd/ft²
1 cd/m²	=	1	10⁻⁴	$π$ ≈ 3.142	10⁷ $π$ ≈ 3.142×10⁷	10³ $π$ ≈ 3.142×10³	10⁻⁴ $π$ ≈ 3.142×10⁻⁴	0.3048² $π$ ≈ 0.2919
1 sb	=	10⁴	1	10⁴ $π$ ≈ 3.142×10⁴	10¹¹ $π$ ≈ 3.142×10¹¹	10⁷ $π$ ≈ 3.142×10⁷	$π$ ≈ 3.142	30.48² $π$ ≈ 2919
1 asb	=	1 ⁄ $π$ ≈ 0.3183	10⁻⁴⁄ $π$ ≈ 3.183×10⁻⁵	1	10⁷	10³	10⁻⁴	0.3048² ≈ 0.09290
1 bril	=	10⁻⁷⁄ $π$ ≈ 3.183×10⁻⁸	10⁻¹¹⁄ $π$ ≈ 3.183×10⁻¹²	10⁻⁷	1	10⁻⁴	10⁻¹¹	0.3048²×10⁻⁷ ≈ 9.290×10⁻⁹
1 sk	=	10⁻³⁄ $π$ ≈ 3.183×10⁻⁴	10⁻⁷⁄ $π$ ≈ 3.183×10⁻⁸	10⁻³	10⁴	1	10⁻⁷	0.3048²×10⁻³ ≈ 9.290×10⁻⁵
1 L	=	10⁴⁄ $π$ ≈ 3183	1 ⁄ $π$ ≈ 0.3183	10⁴	10¹¹	10⁷	1	0.3048²×10⁴ ≈ 929.0
1 fL	=	1 ⁄ 0.3048²⁄ $π$ ≈ 3.426	1 ⁄ 30.48²⁄ $π$ ≈ 3.426×10⁻⁴	1 ⁄ 0.3048² ≈ 10.76	10⁷⁄ 0.3048² ≈ 1.076×10⁸	10³⁄ 0.3048² ≈ 1.076×10⁴	10⁻⁴⁄ 0.3048² ≈ 1.076×10⁻³	1

Related Research Articles

<span class="mw-page-title-main">Candela</span> SI unit of luminous intensity

The candela is the unit of luminous intensity in the International System of Units (SI). It measures luminous power per unit solid angle emitted by a light source in a particular direction. Luminous intensity is analogous to radiant intensity, but instead of simply adding up the contributions of every wavelength of light in the source's spectrum, the contribution of each wavelength is weighted by the luminous efficiency function, the model of the sensitivity of the human eye to different wavelengths, standardized by the CIE and ISO. A common wax candle emits light with a luminous intensity of roughly one candela. If emission in some directions is blocked by an opaque barrier, the emission would still be approximately one candela in the directions that are not obscured.

In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted $σ$ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distance $r$ along the radial line connecting the point to the fixed point of origin; the polar angle $θ$ between the radial line and a given polar axis; and the azimuthal angle $φ$ as the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the reference plane (sometimes fundamental plane).

In optics, Lambert's cosine law says that the observed radiant intensity or luminous intensity from an ideal diffusely reflecting surface or ideal diffuse radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal; I = I₀ cos θ. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert, from his Photometria, published in 1760.

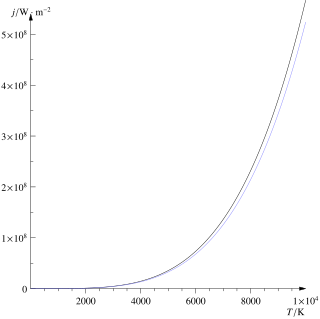
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.

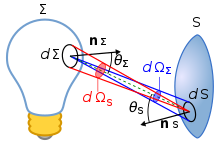
In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.

An infinitesimal rotation matrix or differential rotation matrix is a matrix representing an infinitely small rotation.

In optical physics, transmittance of the surface of a material is its effectiveness in transmitting radiant energy. It is the fraction of incident electromagnetic power that is transmitted through a sample, in contrast to the transmission coefficient, which is the ratio of the transmitted to incident electric field.

In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiation, and to quantify emission of neutrinos and other particles. The SI unit of radiance is the watt per steradian per square metre. It is a directional quantity: the radiance of a surface depends on the direction from which it is being observed.

In classical electromagnetism, polarization density is the vector field that expresses the volumetric density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is said to be polarized.

In photometry, illuminance is the total luminous flux incident on a surface, per unit area. It is a measure of how much the incident light illuminates the surface, wavelength-weighted by the luminosity function to correlate with human brightness perception. Similarly, luminous emittance is the luminous flux per unit area emitted from a surface. Luminous emittance is also known as luminous exitance.

In quantum physics, the scattering amplitude is the probability amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process. At large distances from the centrally symmetric scattering center, the plane wave is described by the wavefunction

Etendue or étendue is a property of light in an optical system, which characterizes how "spread out" the light is in area and angle. It corresponds to the beam parameter product (BPP) in Gaussian beam optics. Other names for etendue include acceptance, throughput, light grasp, light-gathering power, optical extent, and the AΩ product. Throughput and AΩ product are especially used in radiometry and radiative transfer where it is related to the view factor. It is a central concept in nonimaging optics.

Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.

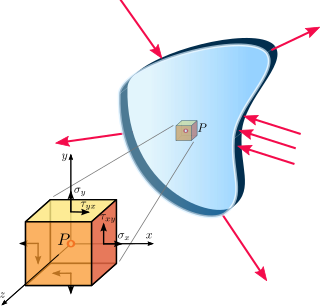
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.

Glare is difficulty of seeing in the presence of bright light such as direct or reflected sunlight or artificial light such as car headlamps at night. Because of this, some cars include mirrors with automatic anti-glare functions and in buildings, blinds or louvers are often used to protect occupants. Glare is caused by a significant ratio of luminance between the task and the glare source. Factors such as the angle between the task and the glare source and eye adaptation have significant impacts on the experience of glare.

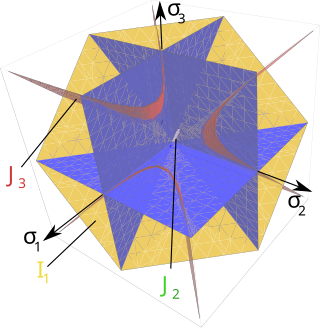
<span class="mw-page-title-main">Yield surface</span> Geometric representation of material yield

A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.

In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.

In physics, and especially scattering theory, the momentum-transfer cross section is an effective scattering cross section useful for describing the average momentum transferred from a particle when it collides with a target. Essentially, it contains all the information about a scattering process necessary for calculating average momentum transfers but ignores other details about the scattering angle.

<span class="mw-page-title-main">Lode coordinates</span>

Lode coordinates $or Haigh-Westergaard coordinates . are a set of tensor invariants that span the space of real, symmetric, second-order, 3-dimensional tensors and are isomorphic with respect to principal stress space. This right-handed orthogonal coordinate system is named in honor of the German scientist Dr. Walter Lode because of his seminal paper written in 1926 describing the effect of the middle principal stress on metal plasticity. Other examples of sets of tensor invariants are the set of principal stresses or the set of kinematic invariants . The Lode coordinate system can be described as a cylindrical coordinate system within principal stress space with a coincident origin and the z-axis parallel to the vector .$

References

↑ "luminance, 17-21-050". CIE S 017:2020 ILV: International Lighting Vocabulary, 2nd edition. CIE - International Commission on Illumination. 2020. Retrieved 20 April 2023.
↑ ISO/CIE 23539:2023 CIE TC 2-93 Photometry — The CIE system of physical photometry. ISO/CIE. 2023. doi:10.25039/IS0.CIE.23539.2023.
↑ "Luminance". Lighting Design Glossary. Retrieved Apr 13, 2009.
↑ Dörband, Bernd; Gross, Herbert; Müller, Henriette (2012). Gross, Herbert (ed.). Handbook of Optical Systems. Vol. 5, Metrology of Optical Components and Systems. Wiley. p. 326. ISBN 978-3-527-40381-3.
↑ IEC 60825-1:2014 Safety of laser products - Part 1: Equipment classification and requirements (in English, French, and Spanish) (3rd ed.). International Electrotechnical Commission. 2014-05-15. p. 220. - TC 76 - Optical radiation safety and laser equipment
↑ "e-ILV : Luminance meter". CIE. Archived from the original on 16 September 2017. Retrieved 20 February 2013.
↑ Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. p. 679. ISBN 978-1482206739. Archived from the original on 2016-02-18.

External links

A Kodak guide to Estimating Luminance and Illuminance using a camera's exposure meter. Also available in PDF form.
Autodesk Design Academy Measuring Light Levels

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[note-dimension-symbol-8] The symbols in this column denote dimensions; "L", "T" and "J" are for length, time and luminous intensity respectively, not the symbols for the units litre, tesla and joule.

[note-suffix-v-9] Standards organizations recommend that photometric quantities be denoted with a subscript "v" (for "visual") to avoid confusion with radiometric or photon quantities. For example: USA Standard Letter Symbols for Illuminating Engineering USAS Z7.1-1967, Y10.18-1967

[note-alternative-symbol-photometric-10] 1 2 3 Alternative symbols sometimes seen: $W$ for luminous energy, $P$ or $F$ for luminous flux, and $ρ$ for luminous efficacy of a source.

[1] "luminance, 17-21-050". CIE S 017:2020 ILV: International Lighting Vocabulary, 2nd edition. CIE - International Commission on Illumination. 2020. Retrieved 20 April 2023.

[2] ISO/CIE 23539:2023 CIE TC 2-93 Photometry — The CIE system of physical photometry. ISO/CIE. 2023. doi:10.25039/IS0.CIE.23539.2023.

[3] "Luminance". Lighting Design Glossary. Retrieved Apr 13, 2009.

[4] Dörband, Bernd; Gross, Herbert; Müller, Henriette (2012). Gross, Herbert (ed.). Handbook of Optical Systems. Vol. 5, Metrology of Optical Components and Systems. Wiley. p. 326. ISBN 978-3-527-40381-3.

[iec-2060825-1-5] IEC 60825-1:2014 Safety of laser products - Part 1: Equipment classification and requirements (in English, French, and Spanish) (3rd ed.). International Electrotechnical Commission. 2014-05-15. p. 220. - TC 76 - Optical radiation safety and laser equipment

[6] "e-ILV : Luminance meter". CIE. Archived from the original on 16 September 2017. Retrieved 20 February 2013.

[7] Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. p. 679. ISBN 978-1482206739. Archived from the original on 2016-02-18.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[nb 1]

[nb 2]

[nb 3]

Quantity		Unit		Dimension ^{[nb 1]}	Notes
Name	Symbol^{[nb 2]}	Name	Symbol	Dimension ^{[nb 1]}	Notes
Luminous energy	$Q v$ ^{[nb 3]}	lumen second	lm⋅s	T⋅J	The lumen second is sometimes called the talbot.
Luminous flux, luminous power	$Φ v$ ^{[nb 3]}	lumen (= candela steradian)	lm (= cd⋅sr)	J	Luminous energy per unit time
Luminous intensity	$I v$	candela (= lumen per steradian)	cd (= lm/sr)	J	Luminous flux per unit solid angle
Luminance	$L v$	candela per square metre	cd/m² (= lm/(sr⋅m²))	L⁻²⋅J	Luminous flux per unit solid angle per unit projected source area. The candela per square metre is sometimes called the nit .
Illuminance	$E v$	lux (= lumen per square metre)	lx (= lm/m²)	L⁻²⋅J	Luminous flux incident on a surface
Luminous exitance, luminous emittance	$M v$	lumen per square metre	lm/m²	L⁻²⋅J	Luminous flux emitted from a surface
Luminous exposure	$H v$	lux second	lx⋅s	L⁻²⋅T⋅J	Time-integrated illuminance
Luminous energy density	$ω v$	lumen second per cubic metre	lm⋅s/m³	L⁻³⋅T⋅J
Luminous efficacy (of radiation)	$K$	lumen per watt	lm/W	M⁻¹⋅L⁻²⋅T³⋅J	Ratio of luminous flux to radiant flux
Luminous efficacy (of a source)	$η$ ^{[nb 3]}	lumen per watt	lm/W	M⁻¹⋅L⁻²⋅T³⋅J	Ratio of luminous flux to power consumption
Luminous efficiency, luminous coefficient	$V$			1	Luminous efficacy normalized by the maximum possible efficacy
See also: SI Photometry Radiometry