The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values
In electromagnetism, the magnetic susceptibility is a measure of how much a material will become magnetized in an applied magnetic field. It is the ratio of magnetization M to the applied magnetizing field intensity H. This allows a simple classification, into two categories, of most materials' responses to an applied magnetic field: an alignment with the magnetic field, χ > 0, called paramagnetism, or an alignment against the field, χ < 0, called diamagnetism.

In electromagnetism, the Mie solution to Maxwell's equations describes the scattering of an electromagnetic plane wave by a homogeneous sphere. The solution takes the form of an infinite series of spherical multipole partial waves. It is named after German physicist Gustav Mie.
The nuclear Overhauser effect (NOE) is the transfer of nuclear spin polarization from one population of spin-active nuclei to another via cross-relaxation. A phenomenological definition of the NOE in nuclear magnetic resonance spectroscopy (NMR) is the change in the integrated intensity of one NMR resonance that occurs when another is saturated by irradiation with an RF field. The change in resonance intensity of a nucleus is a consequence of the nucleus being close in space to those directly affected by the RF perturbation.

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate energy levels and the resulting splittings in those energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.
Nuclear quadrupole resonance spectroscopy or NQR is a chemical analysis technique related to nuclear magnetic resonance (NMR). Unlike NMR, NQR transitions of nuclei can be detected in the absence of a magnetic field, and for this reason NQR spectroscopy is referred to as "zero Field NMR". The NQR resonance is mediated by the interaction of the electric field gradient (EFG) with the quadrupole moment of the nuclear charge distribution. Unlike NMR, NQR is applicable only to solids and not liquids, because in liquids the electric field gradient at the nucleus averages to zero. Because the EFG at the location of a nucleus in a given substance is determined primarily by the valence electrons involved in the particular bond with other nearby nuclei, the NQR frequency at which transitions occur is unique for a given substance. A particular NQR frequency in a compound or crystal is proportional to the product of the nuclear quadrupole moment, a property of the nucleus, and the EFG in the neighborhood of the nucleus. It is this product which is termed the nuclear quadrupole coupling constant for a given isotope in a material and can be found in tables of known NQR transitions. In NMR, an analogous but not identical phenomenon is the coupling constant, which is also the result of an internuclear interaction between nuclei in the analyte.
In physics, the gyromagnetic ratio of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol γ, gamma. Its SI unit is the radian per second per tesla (rad⋅s−1⋅T−1) or, equivalently, the coulomb per kilogram (C⋅kg−1).

Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It was developed by Gingold and Monaghan and Lucy in 1977, initially for astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography. It is a meshfree Lagrangian method, and the resolution of the method can easily be adjusted with respect to variables such as density.

Nuclear magnetic resonance spectroscopy, most commonly known as NMR spectroscopy or magnetic resonance spectroscopy (MRS), is a spectroscopic technique based on re-orientation of atomic nuclei with non-zero nuclear spins in an external magnetic field. This re-orientation occurs with absorption of electromagnetic radiation in the radio frequency region from roughly 4 to 900 MHz, which depends on the isotopic nature of the nucleus and increased proportionally to the strength of the external magnetic field. Notably, the resonance frequency of each NMR-active nucleus depends on its chemical environment. As a result, NMR spectra provide information about individual functional groups present in the sample, as well about connections between nearby nuclei in the same molecule. As the NMR spectra are unique or highly characteristic to individual compounds and functional groups, NMR spectroscopy is one of the most important methods to identify molecular structures, particularly of organic compounds.

Solid-state NMR (ssNMR) spectroscopy is a technique for characterizing atomic level structure in solid materials e.g. powders, single crystals and amorphous samples and tissues using nuclear magnetic resonance (NMR) spectroscopy. The anisotropic part of many spin interactions are present in solid-state NMR, unlike in solution-state NMR where rapid tumbling motion averages out many of the spin interactions. As a result, solid-state NMR spectra are characterised by larger linewidths than in solution state NMR, which can be utilized to give quantitative information on the molecular structure, conformation and dynamics of the material. Solid-state NMR is often combined with magic angle spinning to remove anisotropic interactions and improve the resolution as well as the sensitivity of the technique.
Coherent control is a quantum mechanics-based method for controlling dynamic processes by light. The basic principle is to control quantum interference phenomena, typically by shaping the phase of laser pulses. The basic ideas have proliferated, finding vast application in spectroscopy mass spectra, quantum information processing, laser cooling, ultracold physics and more.
In MRI and NMR spectroscopy, an observable nuclear spin polarization (magnetization) is created by a homogeneous magnetic field. This field makes the magnetic dipole moments of the sample precess at the resonance (Larmor) frequency of the nuclei. At thermal equilibrium, nuclear spins precess randomly about the direction of the applied field. They become abruptly phase coherent when they are hit by radiofrequency (RF) pulses at the resonant frequency, created orthogonal to the field. The RF pulses cause the population of spin-states to be perturbed from their thermal equilibrium value. The generated transverse magnetization can then induce a signal in an RF coil that can be detected and amplified by an RF receiver. The return of the longitudinal component of the magnetization to its equilibrium value is termed spin-latticerelaxation while the loss of phase-coherence of the spins is termed spin-spin relaxation, which is manifest as an observed free induction decay (FID).

Nuclear magnetic resonance quantum computing (NMRQC) is one of the several proposed approaches for constructing a quantum computer, that uses the spin states of nuclei within molecules as qubits. The quantum states are probed through the nuclear magnetic resonances, allowing the system to be implemented as a variation of nuclear magnetic resonance spectroscopy. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems, in this case molecules, rather than a single pure state.
The Hamiltonian is a function used to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain time period. Inspired by—but distinct from—the Hamiltonian of classical mechanics, the Hamiltonian of optimal control theory was developed by Lev Pontryagin as part of his maximum principle. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control should be chosen so as to optimize the Hamiltonian.
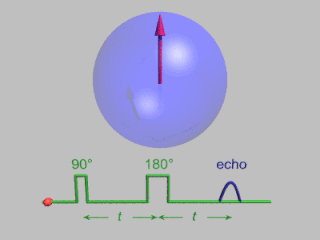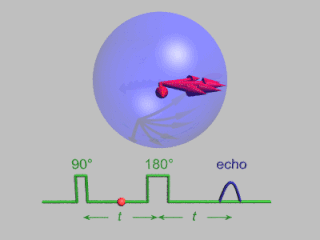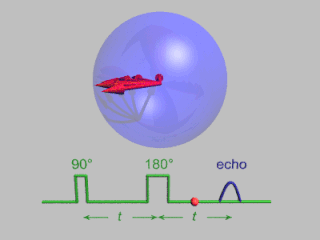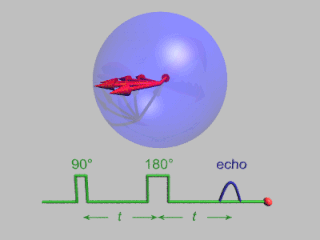
In magnetic resonance, a spin echo or Hahn echo is the refocusing of spin magnetisation by a pulse of resonant electromagnetic radiation. Modern nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) make use of this effect.
During nuclear magnetic resonance observations, spin–lattice relaxation is the mechanism by which the longitudinal component of the total nuclear magnetic moment vector (parallel to the constant magnetic field) exponentially relaxes from a higher energy, non-equilibrium state to thermodynamic equilibrium with its surroundings (the "lattice"). It is characterized by the spin–lattice relaxation time, a time constant known as T1.
Nuclear magnetic resonance (NMR) in porous materials covers the application of using NMR as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity and pore size distribution, the permeability, the water saturation, the wettability, etc.

Nuclear magnetic resonance (NMR) is a physical phenomenon in which nuclei in a strong constant magnetic field are perturbed by a weak oscillating magnetic field and respond by producing an electromagnetic signal with a frequency characteristic of the magnetic field at the nucleus. This process occurs near resonance, when the oscillation frequency matches the intrinsic frequency of the nuclei, which depends on the strength of the static magnetic field, the chemical environment, and the magnetic properties of the isotope involved; in practical applications with static magnetic fields up to ca. 20 tesla, the frequency is similar to VHF and UHF television broadcasts (60–1000 MHz). NMR results from specific magnetic properties of certain atomic nuclei. Nuclear magnetic resonance spectroscopy is widely used to determine the structure of organic molecules in solution and study molecular physics and crystals as well as non-crystalline materials. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI). The original application of NMR to condensed matter physics is nowadays mostly devoted to strongly correlated electron systems. It reveals large manybody couplings by fast broadband detection and it should not to be confused with solid state NMR, which aims at removing the effect of the same couplings by Magic Angle Spinning techniques.
In NMR spectroscopy, the product operator formalism is a method used to determine the outcome of pulse sequences in a rigorous but straightforward way. With this method it is possible to predict how the bulk magnetization evolves with time under the action of pulses applied in different directions. It is a net improvement from the semi-classical vector model which is not able to predict many of the results in NMR spectroscopy and is a simplification of the complete density matrix formalism.

Ilya Kuprov is a British physicist whose research focuses on quantum theory of magnetic processes and nuclear magnetic resonance. Kuprov is a professor of physics at the School of Chemistry of the University of Southampton, a deputy editor of Science Advances, a Fellow of the Royal Society of Chemistry, and a Fellow of the International Society of Magnetic Resonance.

















