
Superparamagnetism is a form of magnetism which appears in small ferromagnetic or ferrimagnetic nanoparticles. In sufficiently small nanoparticles, magnetization can randomly flip direction under the influence of temperature. The typical time between two flips is called the Néel relaxation time. In the absence of an external magnetic field, when the time used to measure the magnetization of the nanoparticles is much longer than the Néel relaxation time, their magnetization appears to be in average zero; they are said to be in the superparamagnetic state. In this state, an external magnetic field is able to magnetize the nanoparticles, similarly to a paramagnet. However, their magnetic susceptibility is much larger than that of paramagnets.
The nuclear Overhauser effect (NOE) is the transfer of nuclear spin polarization from one population of spin-active nuclei to another via cross-relaxation. A phenomenological definition of the NOE in nuclear magnetic resonance spectroscopy (NMR) is the change in the integrated intensity of one NMR resonance that occurs when another is saturated by irradiation with an RF field. The change in resonance intensity of a nucleus is a consequence of the nucleus being close in space to those directly affected by the RF perturbation.

In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude of torque the object experiences in a given magnetic field. When the same magnetic field is applied, objects with larger magnetic moments experience larger torques. The strength of this torque depends not only on the magnitude of the magnetic moment but also on its orientation relative to the direction of the magnetic field. Its direction points from the south pole to north pole of the magnet.
Dynamic nuclear polarization (DNP) results from transferring spin polarization from electrons to nuclei, thereby aligning the nuclear spins to the extent that electron spins are aligned. Note that the alignment of electron spins at a given magnetic field and temperature is described by the Boltzmann distribution under the thermal equilibrium. It is also possible that those electrons are aligned to a higher degree of order by other preparations of electron spin order such as: chemical reactions, optical pumping and spin injection. DNP is considered one of several techniques for hyperpolarization. DNP can also be induced using unpaired electrons produced by radiation damage in solids.
In nuclear magnetic resonance (NMR) spectroscopy, the chemical shift is the resonant frequency of an atomic nucleus relative to a standard in a magnetic field. Often the position and number of chemical shifts are diagnostic of the structure of a molecule. Chemical shifts are also used to describe signals in other forms of spectroscopy such as photoemission spectroscopy.

In Fourier transform nuclear magnetic resonance spectroscopy, free induction decay (FID) is the observable nuclear magnetic resonance (NMR) signal generated by non-equilibrium nuclear spin magnetization precessing about the magnetic field. This non-equilibrium magnetization can be created generally by applying a pulse of radio-frequency close to the Larmor frequency of the nuclear spins.
In physics, Larmor precession is the precession of the magnetic moment of an object about an external magnetic field. The phenomenon is conceptually similar to the precession of a tilted classical gyroscope in an external torque-exerting gravitational field. Objects with a magnetic moment also have angular momentum and effective internal electric current proportional to their angular momentum; these include electrons, protons, other fermions, many atomic and nuclear systems, as well as classical macroscopic systems. The external magnetic field exerts a torque on the magnetic moment,
In nuclear chemistry and nuclear physics, J-couplings are mediated through chemical bonds connecting two spins. It is an indirect interaction between two nuclear spins that arises from hyperfine interactions between the nuclei and local electrons. In NMR spectroscopy, J-coupling contains information about relative bond distances and angles. Most importantly, J-coupling provides information on the connectivity of chemical bonds. It is responsible for the often complex splitting of resonance lines in the NMR spectra of fairly simple molecules.
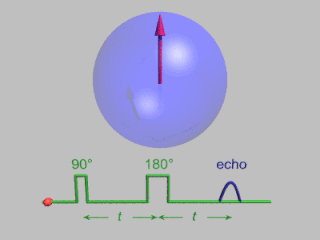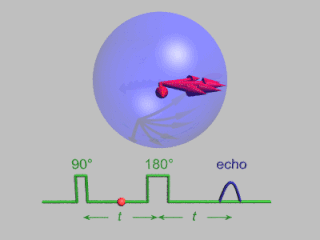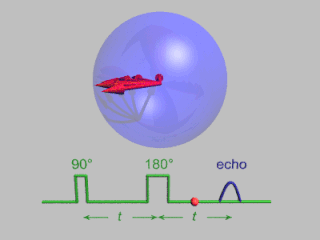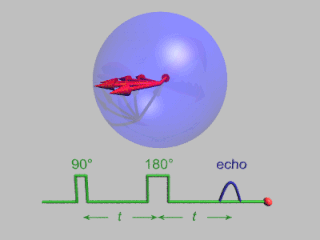
In magnetic resonance, a spin echo or Hahn echo is the refocusing of spin magnetisation by a pulse of resonant electromagnetic radiation. Modern nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) make use of this effect.

In physics, the spin–spin relaxation is the mechanism by which Mxy, the transverse component of the magnetization vector, exponentially decays towards its equilibrium value in nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI). It is characterized by the spin–spin relaxation time, known as T2, a time constant characterizing the signal decay. It is named in contrast to T1, the spin–lattice relaxation time. It is the time it takes for the magnetic resonance signal to irreversibly decay to 37% (1/e) of its initial value after its generation by tipping the longitudinal magnetization towards the magnetic transverse plane. Hence the relation
During nuclear magnetic resonance observations, spin–lattice relaxation is the mechanism by which the longitudinal component of the total nuclear magnetic moment vector (parallel to the constant magnetic field) exponentially relaxes from a higher energy, non-equilibrium state to thermodynamic equilibrium with its surroundings (the "lattice"). It is characterized by the spin–lattice relaxation time, a time constant known as T1.

Zero- to ultralow-field (ZULF) NMR is the acquisition of nuclear magnetic resonance (NMR) spectra of chemicals with magnetically active nuclei in an environment carefully screened from magnetic fields. ZULF NMR experiments typically involve the use of passive or active shielding to attenuate Earth’s magnetic field. This is in contrast to the majority of NMR experiments which are performed in high magnetic fields provided by superconducting magnets. In ZULF experiments the sample is moved through a low field magnet into the "zero field" region where the dominant interactions are nuclear spin-spin couplings, and the coupling between spins and the external magnetic field is a perturbation to this. There are a number of advantages to operating in this regime: magnetic-susceptibility-induced line broadening is attenuated which reduces inhomogeneous broadening of the spectral lines for samples in heterogeneous environments. Another advantage is that the low frequency signals readily pass through conductive materials such as metals due to the increased skin depth; this is not the case for high-field NMR for which the sample containers are usually made of glass, quartz or ceramic. High-field NMR employs inductive detectors to pick up the radiofrequency signals, but this would be inefficient in ZULF NMR experiments since the signal frequencies are typically much lower. The development of highly sensitive magnetic sensors in the early 2000s including SQUIDs, magnetoresistive sensors, and SERF atomic magnetometers made it possible to detect NMR signals directly in the ZULF regime. Previous ZULF NMR experiments relied on indirect detection where the sample had to be shuttled from the shielded ZULF environment into a high magnetic field for detection with a conventional inductive pick-up coil. One successful implementation was using atomic magnetometers at zero magnetic field working with rubidium vapor cells to detect zero-field NMR.
Magnetization transfer (MT), in NMR and MRI, refers to the transfer of nuclear spin polarization and/or spin coherence from one population of nuclei to another population of nuclei, and to techniques that make use of these phenomena. There is some ambiguity regarding the precise definition of magnetization transfer, however the general definition given above encompasses all more specific notions. NMR active nuclei, those with non-zero spin, can be energetically coupled to one another under certain conditions. The mechanisms of nuclear-spin energy-coupling have been extensively characterized and are described in the following articles: Angular momentum coupling, Magnetic dipole–dipole interaction, J-coupling, Residual dipolar coupling, Nuclear Overhauser effect, Spin–spin relaxation, and Spin saturation transfer. Alternatively, some nuclei in a chemical system are labile and exchange between non-equivalent environments. A more specific example of this case is presented in the section Chemical Exchange Magnetization transfer.
In physics and chemistry, specifically in nuclear magnetic resonance (NMR), magnetic resonance imaging (MRI), and electron spin resonance (ESR), the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization M = (Mx, My, Mz) as a function of time when relaxation times T1 and T2 are present. These are phenomenological equations that were introduced by Felix Bloch in 1946. Sometimes they are called the equations of motion of nuclear magnetization. They are analogous to the Maxwell–Bloch equations.
In physics, magnetization dynamics is the branch of solid-state physics that describes the evolution of the magnetization of a material.
Nuclear magnetic resonance (NMR) in porous materials covers the application of using NMR as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity and pore size distribution, the permeability, the water saturation, the wettability, etc.

Nuclear magnetic resonance (NMR) is a physical phenomenon in which nuclei in a strong constant magnetic field are perturbed by a weak oscillating magnetic field and respond by producing an electromagnetic signal with a frequency characteristic of the magnetic field at the nucleus. This process occurs near resonance, when the oscillation frequency matches the intrinsic frequency of the nuclei, which depends on the strength of the static magnetic field, the chemical environment, and the magnetic properties of the isotope involved; in practical applications with static magnetic fields up to ca. 20 tesla, the frequency is similar to VHF and UHF television broadcasts (60–1000 MHz). NMR results from specific magnetic properties of certain atomic nuclei. High-resolution nuclear magnetic resonance spectroscopy is widely used to determine the structure of organic molecules in solution and study molecular physics and crystals as well as non-crystalline materials. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI). The original application of NMR to condensed matter physics is nowadays mostly devoted to strongly correlated electron systems. It reveals large many-body couplings by fast broadband detection and should not be confused with solid state NMR, which aims at removing the effect of the same couplings by Magic Angle Spinning techniques.

Magnetic resonance imaging (MRI) is a medical imaging technique mostly used in radiology and nuclear medicine in order to investigate the anatomy and physiology of the body, and to detect pathologies including tumors, inflammation, neurological conditions such as stroke, disorders of muscles and joints, and abnormalities in the heart and blood vessels among others. Contrast agents may be injected intravenously or into a joint to enhance the image and facilitate diagnosis. Unlike CT and X-ray, MRI uses no ionizing radiation and is, therefore, a safe procedure suitable for diagnosis in children and repeated runs. Patients with specific non-ferromagnetic metal implants, cochlear implants, and cardiac pacemakers nowadays may also have an MRI in spite of effects of the strong magnetic fields. This does not apply on older devices, and details for medical professionals are provided by the device's manufacturer.

Pulsed electron paramagnetic resonance (EPR) is an electron paramagnetic resonance technique that involves the alignment of the net magnetization vector of the electron spins in a constant magnetic field. This alignment is perturbed by applying a short oscillating field, usually a microwave pulse. One can then measure the emitted microwave signal which is created by the sample magnetization. Fourier transformation of the microwave signal yields an EPR spectrum in the frequency domain. With a vast variety of pulse sequences it is possible to gain extensive knowledge on structural and dynamical properties of paramagnetic compounds. Pulsed EPR techniques such as electron spin echo envelope modulation (ESEEM) or pulsed electron nuclear double resonance (ENDOR) can reveal the interactions of the electron spin with its surrounding nuclear spins.
In quantum mechanics, magnetic resonance is a resonant effect that can appear when a magnetic dipole is exposed to a static magnetic field and perturbed with another, oscillating electromagnetic field. Due to the static field, the dipole can assume a number of discrete energy eigenstates, depending on the value of its angular momentum (azimuthal) quantum number. The oscillating field can then make the dipole transit between its energy states with a certain probability and at a certain rate. The overall transition probability will depend on the field's frequency and the rate will depend on its amplitude. When the frequency of that field leads to the maximum possible transition probability between two states, a magnetic resonance has been achieved. In that case, the energy of the photons composing the oscillating field matches the energy difference between said states. If the dipole is tickled with a field oscillating far from resonance, it is unlikely to transition. That is analogous to other resonant effects, such as with the forced harmonic oscillator. The periodic transition between the different states is called Rabi cycle and the rate at which that happens is called Rabi frequency. The Rabi frequency should not be confused with the field's own frequency. Since many atomic nuclei species can behave as a magnetic dipole, this resonance technique is the basis of nuclear magnetic resonance, including nuclear magnetic resonance imaging and nuclear magnetic resonance spectroscopy.











































