Nuclear magnetic resonance quantum computer

Last updated November 25, 2023

Molecule of alanine used in NMR implementation of quantum computing. Qubits are implemented by spin states of the black carbon atoms L-alanine-3D-balls.png — Molecule of alanine used in NMR implementation of quantum computing. Qubits are implemented by spin states of the black carbon atoms

Nuclear magnetic resonance quantum computing (NMRQC)^[1] is one of the several proposed approaches for constructing a quantum computer, that uses the spin states of nuclei within molecules as qubits. The quantum states are probed through the nuclear magnetic resonances, allowing the system to be implemented as a variation of nuclear magnetic resonance spectroscopy. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems, in this case molecules, rather than a single pure state.

Liquid state NMR

The ideal picture of liquid state NMR (LSNMR) quantum information processing (QIP) is based on a molecule in which some of its atom's nuclei behave as spin-½ systems.^[2] Depending on which nuclei we are considering they will have different energy levels and different interaction with its neighbours and so we can treat them as distinguishable qubits. In this system we tend to consider the inter-atomic bonds as the source of interactions between qubits and exploit these spin-spin interactions to perform 2-qubit gates such as CNOTs that are necessary for universal quantum computation. In addition to the spin-spin interactions native to the molecule an external magnetic field can be applied (in NMR laboratories) and these impose single qubit gates. By exploiting the fact that different spins will experience different local fields we have control over the individual spins.

The picture described above is far from realistic since we are treating a single molecule. NMR is performed on an ensemble of molecules, usually with as many as 10^15 molecules. This introduces complications to the model, one of which is introduction of decoherence. In particular we have the problem of an open quantum system interacting with a macroscopic number of particles near thermal equilibrium (~mK to ~300 K). This has led the development of decoherence suppression techniques that have spread to other disciplines such as trapped ions. The other significant issue with regards to working close to thermal equilibrium is the mixedness of the state. This required the introduction of ensemble quantum processing, whose principal limitation is that as we introduce more logical qubits into our system we require larger samples in order to attain discernable signals during measurement.

Solid state NMR

Solid state NMR (SSNMR), unlike LSNMR uses a solid state sample, for example a nitrogen vacancy diamond lattice rather than a liquid sample.^[3] This has many advantages such as lack of molecular diffusion decoherence, lower temperatures can be achieved to the point of suppressing phonon decoherence and a greater variety of control operations that allow us to overcome one of the major problems of LSNMR that is initialisation. Moreover, as in a crystal structure we can localize precisely the qubits, we can measure each qubit individually, instead of having an ensemble measurement as in LSNMR.

History

The use of nuclear spins for quantum computing was first discussed by Seth Lloyd and by David DiVincenzo.^[4]^[5]^[6] Manipulation of nuclear spins for quantum computing using liquid state NMR was introduced independently by Cory, Fahmy and Havel^[7]^[8] and Gershenfeld and Chuang ^[9] in 1997. Some early success was obtained in performing quantum algorithms in NMR systems due to the relative maturity of NMR technology. For instance, in 2001 researchers at IBM reported the successful implementation of Shor's algorithm in a 7-qubit NMR quantum computer.^[10] However, even from the early days, it was recognized that NMR quantum computers would never be very useful due to the poor scaling of the signal-to-noise ratio in such systems.^[11] More recent work, particularly by Caves and others, shows that all experiments in liquid state bulk ensemble NMR quantum computing to date do not possess quantum entanglement, thought to be required for quantum computation. Hence NMR quantum computing experiments are likely to have been only classical simulations of a quantum computer.^[12]

Mathematical representation

The ensemble is initialized to be the thermal equilibrium state (see quantum statistical mechanics). In mathematical parlance, this state is given by the density matrix:

\rho ={\frac {e^{-\beta H}}{\operatorname {Tr} (e^{-\beta H})}},

where H is the hamiltonian matrix of an individual molecule and

\beta ={\frac {1}{k\,T}}

where $k$ is the Boltzmann constant and $T$ the temperature. That the initial state in NMR quantum computing is in thermal equilibrium is one of the main differences compared to other quantum computing techniques, where they are initialized in a pure state. Nevertheless, suitable mixed states are capable of reflecting quantum dynamics which lead to Gershenfeld and Chuang to term them "pseudo-pure states."^[9]

Operations are performed on the ensemble through radio frequency (RF) pulses applied perpendicular to a strong, static magnetic field, created by a very large magnet. See nuclear magnetic resonance.

Consider applying a magnetic field along the z axis, fixing this as the principal quantization axis, on a liquid sample. The Hamiltonian for a single spin would be given by the Zeeman or chemical shift term:

H=\mu B_{z}=I_{z}\omega

where $I_{z}$ is the operator for the z component of the nuclear angular momentum, and $\omega$ is the resonance frequency of the spin, which is proportional to the applied magnetic field.

Considering the molecules in the liquid sample to contain two spin ½ nuclei, the system Hamiltonian will have two chemical shift terms and a dipole coupling term:

H=\omega _{1}I_{z1}+\omega _{2}I_{z2}+2J_{12}I_{z1}I_{z2}

Control of a spin system can be realized by means of selective RF pulses applied perpendicular to the quantization axis. In the case of a two spin system as described above, we can distinguish two types of pulses: “soft” or spin-selective pulses, whose frequency range encompasses one of the resonant frequencies only, and therefore affects only that spin; and “hard” or nonselective pulses whose frequency range is broad enough to contain both resonant frequencies and therefore these pulses couple to both spins. For detailed examples of the effects of pulses on such a spin system, the reader is referred to Section 2 of work by Cory et al.^[13]

Related Research Articles

In quantum computing, a qubit or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state quantum-mechanical system, one of the simplest quantum systems displaying the peculiarity of quantum mechanics. Examples include the spin of the electron in which the two levels can be taken as spin up and spin down; or the polarization of a single photon in which the two states can be taken to be the vertical and the horizontal polarization. In a classical system, a bit would have to be in one state or the other. However, quantum mechanics allows the qubit to be in a coherent superposition of both states simultaneously, a property that is fundamental to quantum mechanics and quantum computing.

This is a timeline of quantum computing.

The Kane quantum computer is a proposal for a scalable quantum computer proposed by Bruce Kane in 1998, who was then at the University of New South Wales. Often thought of as a hybrid between quantum dot and nuclear magnetic resonance (NMR) quantum computers, the Kane computer is based on an array of individual phosphorus donor atoms embedded in a pure silicon lattice. Both the nuclear spins of the donors and the spins of the donor electrons participate in the computation.

Dynamic nuclear polarization (DNP) results from transferring spin polarization from electrons to nuclei, thereby aligning the nuclear spins to the extent that electron spins are aligned. Note that the alignment of electron spins at a given magnetic field and temperature is described by the Boltzmann distribution under the thermal equilibrium. It is also possible that those electrons are aligned to a higher degree of order by other preparations of electron spin order such as: chemical reactions, optical pumping and spin injection. DNP is considered one of several techniques for hyperpolarization. DNP can also be induced using unpaired electrons produced by radiation damage in solids.

Superconducting quantum computing is a branch of solid state quantum computing that implements superconducting electronic circuits using superconducting qubits as artificial atoms, or quantum dots. For superconducting qubits, the two logic states are the ground state and the excited state, denoted $respectively. Research in superconducting quantum computing is conducted by companies such as Google, IBM, IMEC, BBN Technologies, Rigetti, and Intel. Many recently developed QPUs utilize superconducting architecture.$

<span class="mw-page-title-main">Nuclear magnetic resonance spectroscopy</span> Laboratory technique

Nuclear magnetic resonance spectroscopy, most commonly known as NMR spectroscopy or magnetic resonance spectroscopy (MRS), is a spectroscopic technique based on re-orientation of atomic nuclei with non-zero nuclear spins in an external magnetic field. This re-orientation occurs with absorption of electromagnetic radiation in the radio frequency region from roughly 4 to 900 MHz, which depends on the isotopic nature of the nucleus and increased proportionally to the strength of the external magnetic field. Notably, the resonance frequency of each NMR-active nucleus depends on its chemical environment. As a result, NMR spectra provide information about individual functional groups present in the sample, as well about connections between nearby nuclei in the same molecule. As the NMR spectra are unique or highly characteristic to individual compounds and functional groups, NMR spectroscopy is one of the most important methods to identify molecular structures, particulary of organic compounds.

Electron paramagnetic resonance (EPR) or electron spin resonance (ESR) spectroscopy is a method for studying materials that have unpaired electrons. The basic concepts of EPR are analogous to those of nuclear magnetic resonance (NMR), but the spins excited are those of the electrons instead of the atomic nuclei. EPR spectroscopy is particularly useful for studying metal complexes and organic radicals. EPR was first observed in Kazan State University by Soviet physicist Yevgeny Zavoisky in 1944, and was developed independently at the same time by Brebis Bleaney at the University of Oxford.

Solid-state NMR (ssNMR) spectroscopy is a technique for characterizing atomic level structure in solid materials e.g. powders, single crystals and amorphous samples and tissues using nuclear magnetic resonance (NMR) spectroscopy. The anisotropic part of many spin interactions are present in solid-state NMR, unlike in solution-state NMR where rapid tumbling motion averages out many of the spin interactions. As a result, solid-state NMR spectra are characterised by larger linewidths than in solution state NMR, which can be utilized to give quantitative information on the molecular structure, conformation and dynamics of the material. Solid-state NMR is often combined with magic angle spinning to remove anisotropic interactions and improve the resolution as well as the sensitivity of the technique.

A trapped-ion quantum computer is one proposed approach to a large-scale quantum computer. Ions, or charged atomic particles, can be confined and suspended in free space using electromagnetic fields. Qubits are stored in stable electronic states of each ion, and quantum information can be transferred through the collective quantized motion of the ions in a shared trap. Lasers are applied to induce coupling between the qubit states or coupling between the internal qubit states and the external motional states.

In MRI and NMR spectroscopy, an observable nuclear spin polarization (magnetization) is created by a homogeneous magnetic field. This field makes the magnetic dipole moments of the sample precess at the resonance (Larmor) frequency of the nuclei. At thermal equilibrium, nuclear spins precess randomly about the direction of the applied field. They become abruptly phase coherent when they are hit by radiofrequency (RF) pulses at the resonant frequency, created orthogonal to the field. The RF pulses cause the population of spin-states to be perturbed from their thermal equilibrium value. The generated transverse magnetization can then induce a signal in an RF coil that can be detected and amplified by an RF receiver. The return of the longitudinal component of the magnetization to its equilibrium value is termed spin-latticerelaxation while the loss of phase-coherence of the spins is termed spin-spin relaxation, which is manifest as an observed free induction decay (FID).

In nuclear chemistry and nuclear physics, J-couplings are mediated through chemical bonds connecting two spins. It is an indirect interaction between two nuclear spins that arises from hyperfine interactions between the nuclei and local electrons. In NMR spectroscopy, J-coupling contains information about relative bond distances and angles. Most importantly, J-coupling provides information on the connectivity of chemical bonds. It is responsible for the often complex splitting of resonance lines in the NMR spectra of fairly simple molecules.

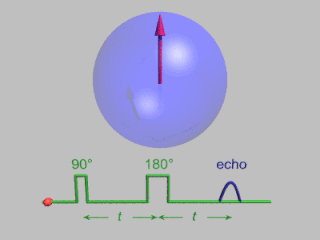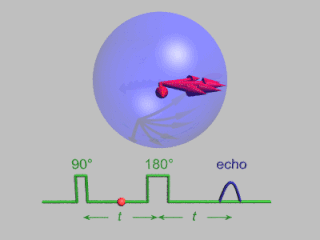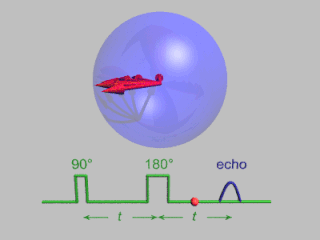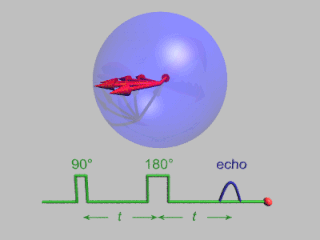
In magnetic resonance, a spin echo or Hahn echo is the refocusing of spin magnetisation by a pulse of resonant electromagnetic radiation. Modern nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) make use of this effect.

The spin qubit quantum computer is a quantum computer based on controlling the spin of charge carriers in semiconductor devices. The first spin qubit quantum computer was first proposed by Daniel Loss and David P. DiVincenzo in 1997, also known as the Loss–DiVincenzo quantum computer. The proposal was to use the intrinsic spin-½ degree of freedom of individual electrons confined in quantum dots as qubits. This should not be confused with other proposals that use the nuclear spin as qubit, like the Kane quantum computer or the nuclear magnetic resonance quantum computer.

Zero- to ultralow-field (ZULF) NMR is the acquisition of nuclear magnetic resonance (NMR) spectra of chemicals with magnetically active nuclei in an environment carefully screened from magnetic fields. ZULF NMR experiments typically involve the use of passive or active shielding to attenuate Earth’s magnetic field. This is in contrast to the majority of NMR experiments which are performed in high magnetic fields provided by superconducting magnets. In ZULF experiments the dominant interactions are nuclear spin-spin couplings, and the coupling between spins and the external magnetic field is a perturbation to this. There are a number of advantages to operating in this regime: magnetic-susceptibility-induced line broadening is attenuated which reduces inhomogeneous broadening of the spectral lines for samples in heterogeneous environments. Another advantage is that the low frequency signals readily pass through conductive materials such as metals due to the increased skin depth; this is not the case for high-field NMR for which the sample containers are usually made of glass, quartz or ceramic.

Nuclear magnetic resonance (NMR) is a physical phenomenon in which nuclei in a strong constant magnetic field are perturbed by a weak oscillating magnetic field and respond by producing an electromagnetic signal with a frequency characteristic of the magnetic field at the nucleus. This process occurs near resonance, when the oscillation frequency matches the intrinsic frequency of the nuclei, which depends on the strength of the static magnetic field, the chemical environment, and the magnetic properties of the isotope involved; in practical applications with static magnetic fields up to ca. 20 tesla, the frequency is similar to VHF and UHF television broadcasts (60–1000 MHz). NMR results from specific magnetic properties of certain atomic nuclei. Nuclear magnetic resonance spectroscopy is widely used to determine the structure of organic molecules in solution and study molecular physics and crystals as well as non-crystalline materials. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI).

Electron nuclear double resonance (ENDOR) is a magnetic resonance technique for elucidating the molecular and electronic structure of paramagnetic species. The technique was first introduced to resolve interactions in electron paramagnetic resonance (EPR) spectra. It is currently practiced in a variety of modalities, mainly in the areas of biophysics and heterogeneous catalysis.

The physics of magnetic resonance imaging (MRI) concerns fundamental physical considerations of MRI techniques and technological aspects of MRI devices. MRI is a medical imaging technique mostly used in radiology and nuclear medicine in order to investigate the anatomy and physiology of the body, and to detect pathologies including tumors, inflammation, neurological conditions such as stroke, disorders of muscles and joints, and abnormalities in the heart and blood vessels among others. Contrast agents may be injected intravenously or into a joint to enhance the image and facilitate diagnosis. Unlike CT and X-ray, MRI uses no ionizing radiation and is, therefore, a safe procedure suitable for diagnosis in children and repeated runs. Patients with specific non-ferromagnetic metal implants, cochlear implants, and cardiac pacemakers nowadays may also have an MRI in spite of effects of the strong magnetic fields. This does not apply on older devices, and details for medical professionals are provided by the device's manufacturer.

Pulsed electron paramagnetic resonance (EPR) is an electron paramagnetic resonance technique that involves the alignment of the net magnetization vector of the electron spins in a constant magnetic field. This alignment is perturbed by applying a short oscillating field, usually a microwave pulse. One can then measure the emitted microwave signal which is created by the sample magnetization. Fourier transformation of the microwave signal yields an EPR spectrum in the frequency domain. With a vast variety of pulse sequences it is possible to gain extensive knowledge on structural and dynamical properties of paramagnetic compounds. Pulsed EPR techniques such as electron spin echo envelope modulation (ESEEM) or pulsed electron nuclear double resonance (ENDOR) can reveal the interactions of the electron spin with its surrounding nuclear spins.

Algorithmic cooling is an algorithmic method for transferring heat from some qubits to others or outside the system and into the environment, which results in a cooling effect. This method uses regular quantum operations on ensembles of qubits, and it can be shown that it can succeed beyond Shannon's bound on data compression. The phenomenon is a result of the connection between thermodynamics and information theory.

The DiVincenzo criteria are conditions necessary for constructing a quantum computer, conditions proposed in 2000 by the theoretical physicist David P. DiVincenzo, as being those necessary to construct such a computer—a computer first proposed by mathematician Yuri Manin, in 1980, and physicist Richard Feynman, in 1982—as a means to efficiently simulate quantum systems, such as in solving the quantum many-body problem.

References

↑ "Nuclear Magnetic Resonance Quantum Computing (NMRQC)".
↑ Neil Gershenfeld; Isaac L. Chuang (1998). "Quantum computing with molecules" (PDF). Scientific American. 278 (6): 66–71. Bibcode:1998SciAm.278f..66G. doi:10.1038/scientificamerican0698-66.
↑ "Diamond Sparkles in Quantum Computing".
↑ Seth Lloyd (1993). "A Potentially Realizable Quantum Computer". Science. 261 (5128): 1569–1571. Bibcode:1993Sci...261.1569L. doi:10.1126/science.261.5128.1569. PMID 17798117. S2CID 38100483.
↑ David DiVincenzo (1995). "A Two-bit gates are universal for quantum computation". Phys. Rev. A. 51 (2): 1015–1022. arXiv: cond-mat/9407022 . Bibcode:1995PhRvA..51.1015D. doi:10.1103/PhysRevA.51.1015. PMID 9911679. S2CID 2317415.
↑ David DiVincenzo (1995). "Quantum computation". Science. 270 (5234).
↑ Cory, David G.; Fahmy, Amr F.; Havel, Timothy F. (1996). "Nuclear Magnetic Resonance Spectroscopy: An Experimentally Accessible Paradigm for Quantum Computing". Phys-Comp 96, Proceedings of the Fourth Workshop on Physics and Computation, edited by T.Toffoli, M.Biafore, and J.Leao (New England Complex Systems Institute. pp. 87–91.
↑ Cory, David G.; Fahmy, Amr F.; Havel, Timothy F. (1997-03-04). "Ensemble quantum computing by NMR spectroscopy". Proceedings of the National Academy of Sciences. 94 (5): 1634–1639. Bibcode:1997PNAS...94.1634C. doi: 10.1073/pnas.94.5.1634 . ISSN 0027-8424. PMC 19968 . PMID 9050830.
1 2 Gershenfeld, Neil A.; Chuang, Isaac L. (1997-01-17). "Bulk Spin-Resonance Quantum Computation". Science. 275 (5298): 350–356. CiteSeerX 10.1.1.28.8877 . doi:10.1126/science.275.5298.350. ISSN 0036-8075. PMID 8994025. S2CID 2262147.
↑ Vandersypen LM, Steffen M, Breyta G, Yannoni CS, Sherwood MH, Chuang IL (2001). "Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance". Nature. 414 (6866): 883–887. arXiv: quant-ph/0112176 . Bibcode:2001Natur.414..883V. doi:10.1038/414883a. PMID 11780055. S2CID 4400832.
↑ Warren WS (1997). "The usefulness of NMR quantum computing". Science. 277 (5332): 1688–1689. doi:10.1126/science.277.5332.1688.
↑ Menicucci NC, Caves CM (2002). "Local realistic model for the dynamics of bulk-ensemble NMR information processing". Physical Review Letters. 88 (16): 167901. arXiv: quant-ph/0111152 . Bibcode:2002PhRvL..88p7901M. doi:10.1103/PhysRevLett.88.167901. PMID 11955265. S2CID 14583916.
↑ Cory D.; et al. (1998). "Nuclear magnetic resonance spectroscopy: An experimentally accessible paradigm for quantum computing". Physica D. 120 (1–2): 82–101. arXiv: quant-ph/9709001 . Bibcode:1998PhyD..120...82C. doi:10.1016/S0167-2789(98)00046-3. S2CID 219400.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] "Nuclear Magnetic Resonance Quantum Computing (NMRQC)".

[2] Neil Gershenfeld; Isaac L. Chuang (1998). "Quantum computing with molecules" (PDF). Scientific American. 278 (6): 66–71. Bibcode:1998SciAm.278f..66G. doi:10.1038/scientificamerican0698-66.

[3] "Diamond Sparkles in Quantum Computing".

[4] Seth Lloyd (1993). "A Potentially Realizable Quantum Computer". Science. 261 (5128): 1569–1571. Bibcode:1993Sci...261.1569L. doi:10.1126/science.261.5128.1569. PMID 17798117. S2CID 38100483.

[5] David DiVincenzo (1995). "A Two-bit gates are universal for quantum computation". Phys. Rev. A. 51 (2): 1015–1022. arXiv: cond-mat/9407022 . Bibcode:1995PhRvA..51.1015D. doi:10.1103/PhysRevA.51.1015. PMID 9911679. S2CID 2317415.

[6] David DiVincenzo (1995). "Quantum computation". Science. 270 (5234).

[7] Cory, David G.; Fahmy, Amr F.; Havel, Timothy F. (1996). "Nuclear Magnetic Resonance Spectroscopy: An Experimentally Accessible Paradigm for Quantum Computing". Phys-Comp 96, Proceedings of the Fourth Workshop on Physics and Computation, edited by T.Toffoli, M.Biafore, and J.Leao (New England Complex Systems Institute. pp. 87–91.

[8] Cory, David G.; Fahmy, Amr F.; Havel, Timothy F. (1997-03-04). "Ensemble quantum computing by NMR spectroscopy". Proceedings of the National Academy of Sciences. 94 (5): 1634–1639. Bibcode:1997PNAS...94.1634C. doi: 10.1073/pnas.94.5.1634 . ISSN 0027-8424. PMC 19968 . PMID 9050830.

[:0-9] 1 2 Gershenfeld, Neil A.; Chuang, Isaac L. (1997-01-17). "Bulk Spin-Resonance Quantum Computation". Science. 275 (5298): 350–356. CiteSeerX 10.1.1.28.8877 . doi:10.1126/science.275.5298.350. ISSN 0036-8075. PMID 8994025. S2CID 2262147.

[10] Vandersypen LM, Steffen M, Breyta G, Yannoni CS, Sherwood MH, Chuang IL (2001). "Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance". Nature. 414 (6866): 883–887. arXiv: quant-ph/0112176 . Bibcode:2001Natur.414..883V. doi:10.1038/414883a. PMID 11780055. S2CID 4400832.

[11] Warren WS (1997). "The usefulness of NMR quantum computing". Science. 277 (5332): 1688–1689. doi:10.1126/science.277.5332.1688.

[12] Menicucci NC, Caves CM (2002). "Local realistic model for the dynamics of bulk-ensemble NMR information processing". Physical Review Letters. 88 (16): 167901. arXiv: quant-ph/0111152 . Bibcode:2002PhRvL..88p7901M. doi:10.1103/PhysRevLett.88.167901. PMID 11955265. S2CID 14583916.

[13] Cory D.; et al. (1998). "Nuclear magnetic resonance spectroscopy: An experimentally accessible paradigm for quantum computing". Physica D. 120 (1–2): 82–101. arXiv: quant-ph/9709001 . Bibcode:1998PhyD..120...82C. doi:10.1016/S0167-2789(98)00046-3. S2CID 219400.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]