
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, is a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just evaluations of the function, where is the size of the function's domain. It was devised by Lov Grover in 1996.
In physics, the Clauser–Horne–Shimony–Holt (CHSH) inequality can be used in the proof of Bell's theorem, which states that certain consequences of entanglement in quantum mechanics cannot be reproduced by local hidden-variable theories. Experimental verification of the inequality being violated is seen as confirmation that nature cannot be described by such theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony, and Richard Holt, who described it in a much-cited paper published in 1969. They derived the CHSH inequality, which, as with John Stewart Bell's original inequality, is a constraint—on the statistical occurrence of "coincidences" in a Bell test—which is necessarily true if an underlying local hidden-variable theory exists. In practice, the inequality is routinely violated by modern experiments in quantum mechanics.

In quantum mechanics, a spherically symmetric potential is a system of which the potential only depends on the radial distance from the spherical center and a location in space. A particle in a spherically symmetric potential will behave accordingly to said potential and can therefore be used as an approximation, for example, of the electron in a hydrogen atom or of the formation of chemical bonds.
The Deutsch–Jozsa algorithm is a deterministic quantum algorithm proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998. Although of little practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.

In physics, the Rabi cycle is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an optical driving field. The effect is important in quantum optics, magnetic resonance, and quantum computing, and is named after Isidor Isaac Rabi.
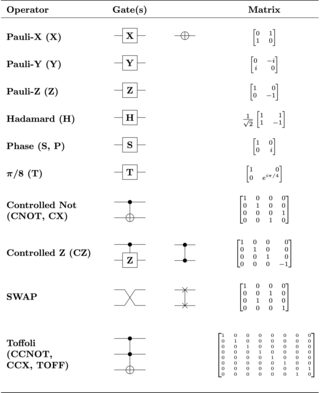
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate is a basic quantum circuit operating on a small number of qubits. Quantum logic gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.
In theoretical physics, supersymmetric quantum mechanics is an area of research where supersymmetry are applied to the simpler setting of plain quantum mechanics, rather than quantum field theory. Supersymmetric quantum mechanics has found applications outside of high-energy physics, such as providing new methods to solve quantum mechanical problems, providing useful extensions to the WKB approximation, and statistical mechanics.
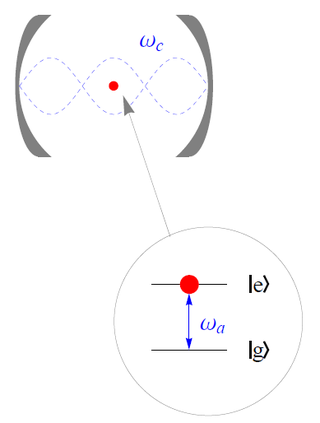
In quantum optics, the Jaynes–Cummings model is a theoretical model that describes the system of a two-level atom interacting with a quantized mode of an optical cavity, with or without the presence of light. It was originally developed to study the interaction of atoms with the quantized electromagnetic field in order to investigate the phenomena of spontaneous emission and absorption of photons in a cavity. It is named after Edwin Thompson Jaynes and Fred Cummings in the 1960s and was confirmed experimentally in 1987.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
Amplitude amplification is a technique in quantum computing which generalizes the idea behind Grover's search algorithm, and gives rise to a family of quantum algorithms. It was discovered by Gilles Brassard and Peter Høyer in 1997, and independently rediscovered by Lov Grover in 1998.
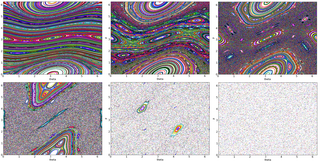
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos and quantum chaos. It describes a free rotating stick in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm to estimate the phase corresponding to an eigenvalue of a given unitary operator. Because the eigenvalues of a unitary operator always have unit modulus, they are characterized by their phase, and therefore the algorithm can be equivalently described as retrieving either the phase or the eigenvalue itself. The algorithm was initially introduced by Alexei Kitaev in 1995.
The Harrow–Hassidim–Lloyd algorithm or HHL algorithm is a quantum algorithm for numerically solving a system of linear equations, designed by Aram Harrow, Avinatan Hassidim, and Seth Lloyd. The algorithm estimates the result of a scalar measurement on the solution vector to a given linear system of equations.
The Peierls substitution method, named after the original work by Rudolf Peierls is a widely employed approximation for describing tightly-bound electrons in the presence of a slowly varying magnetic vector potential.
The KLM scheme or KLM protocol is an implementation of linear optical quantum computing (LOQC) developed in 2000 by Emanuel Knill, Raymond Laflamme and Gerard J. Milburn. This protocol allows for the creation of universal quantum computers using solely linear optical tools. The KLM protocol uses linear optical elements, single-photon sources and photon detectors as resources to construct a quantum computation scheme involving only ancilla resources, quantum teleportations and error corrections.
The quantum Fisher information is a central quantity in quantum metrology and is the quantum analogue of the classical Fisher information. It is one of the central quantities used to qualify the utility of an input state, especially in Mach–Zehnder interferometer-based phase or parameter estimation. It is shown that the quantum Fisher information can also be a sensitive probe of a quantum phase transition. The quantum Fisher information of a state with respect to the observable is defined as
In quantum computing, the variational quantum eigensolver (VQE) is a quantum algorithm for quantum chemistry, quantum simulations and optimization problems. It is a hybrid algorithm that uses both classical computers and quantum computers to find the ground state of a given physical system. Given a guess or ansatz, the quantum processor calculates the expectation value of the system with respect to an observable, often the Hamiltonian, and a classical optimizer is used to improve the guess. The algorithm is based on the variational method of quantum mechanics.
In the context of quantum computing, the quantum walk search is a quantum algorithm for finding a marked node in a graph.
Projection filters are a set of algorithms based on stochastic analysis and information geometry, or the differential geometric approach to statistics, used to find approximate solutions for filtering problems for nonlinear state-space systems. The filtering problem consists of estimating the unobserved signal of a random dynamical system from partial noisy observations of the signal. The objective is computing the probability distribution of the signal conditional on the history of the noise-perturbed observations. This distribution allows for calculations of all statistics of the signal given the history of observations. If this distribution has a density, the density satisfies specific stochastic partial differential equations (SPDEs) called Kushner-Stratonovich equation, or Zakai equation. It is known that the nonlinear filter density evolves in an infinite dimensional function space.











































