In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue to the complexity class BPP.

In quantum mechanics, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, x, and momentum, p, can be predicted from initial conditions.
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, refers to a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just evaluations of the function, where is the size of the function's domain. It was devised by Lov Grover in 1996.
The Deutsch–Jozsa algorithm is a deterministic quantum algorithm proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998. Although of little current practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.
Quantum error correction (QEC) is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is theorised as essential to achieve fault-tolerant quantum computation that can reduce the effects of noise on stored quantum information, faulty quantum gates, faulty quantum preparation, and faulty measurements.
In quantum computing, a graph state is a special type of multi-qubit state that can be represented by a graph. Each qubit is represented by a vertex of the graph, and there is an edge between every interacting pair of qubits. In particular, they are a convenient way of representing certain types of entangled states.
The theory of quantum error correction plays a prominent role in the practical realization and engineering of quantum computing and quantum communication devices. The first quantum error-correcting codes are strikingly similar to classical block codes in their operation and performance. Quantum error-correcting codes restore a noisy, decohered quantum state to a pure quantum state. A stabilizer quantum error-correcting code appends ancilla qubits to qubits that we want to protect. A unitary encoding circuit rotates the global state into a subspace of a larger Hilbert space. This highly entangled, encoded state corrects for local noisy errors. A quantum error-correcting code makes quantum computation and quantum communication practical by providing a way for a sender and receiver to simulate a noiseless qubit channel given a noisy qubit channel whose noise conforms to a particular error model.
The Steane code is a tool in quantum error correction introduced by Andrew Steane in 1996. It is a CSS code (Calderbank-Shor-Steane), using the classical binary [7,4,3] Hamming code to correct for qubit flip errors and the dual of the Hamming code, the [7,3,4] code, to correct for phase flip errors. The Steane code encodes one logical qubit in 7 physical qubits and is able to correct arbitrary single qubit errors.
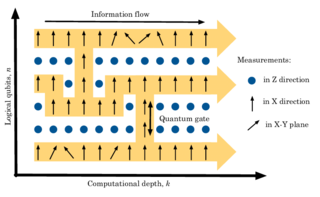
The one-way or measurement-based quantum computer (MBQC) is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.
In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster C is a connected subset of a d-dimensional lattice, and a cluster state is a pure state of the qubits located on C. They are different from other types of entangled states such as GHZ states or W states in that it is more difficult to eliminate quantum entanglement in the case of cluster states. Another way of thinking of cluster states is as a particular instance of graph states, where the underlying graph is a connected subset of a d-dimensional lattice. Cluster states are especially useful in the context of the one-way quantum computer. For a comprehensible introduction to the topic see.
In quantum information theory, mutually unbiased bases in Hilbert space Cd are two orthonormal bases and such that the square of the magnitude of the inner product between any basis states and equals the inverse of the dimension d:
A quantum t-design is a probability distribution over either pure quantum states or unitary operators which can duplicate properties of the probability distribution over the Haar measure for polynomials of degree t or less. Specifically, the average of any polynomial function of degree t over the design is exactly the same as the average over Haar measure. Here the Haar measure is a uniform probability distribution over all quantum states or over all unitary operators. Quantum t-designs are so called because they are analogous to t-designs in classical statistics, which arose historically in connection with the problem of design of experiments. Two particularly important types of t-designs in quantum mechanics are projective and unitary t-designs.
Entanglement distillation is the transformation of N copies of an arbitrary entangled state into some number of approximately pure Bell pairs, using only local operations and classical communication.
Quantum block codes are useful in quantum computing and in quantum communications. The encoding circuit for a large block code typically has a high complexity although those for modern codes do have lower complexity.
The toric code is a topological quantum error correcting code, and an example of a stabilizer code, defined on a two-dimensional spin lattice. It is the simplest and most well studied of the quantum double models. It is also the simplest example of topological order—Z2 topological order (first studied in the context of Z2 spin liquid in 1991). The toric code can also be considered to be a Z2 lattice gauge theory in a particular limit. It was introduced by Alexei Kitaev.
In quantum mechanics, the cat state, named after Schrödinger's cat, is a quantum state composed of two diametrically opposed conditions at the same time, such as the possibilities that a cat is alive and dead at the same time.
The quantum algorithm for linear systems of equations, also called HHL algorithm, designed by Aram Harrow, Avinatan Hassidim, and Seth Lloyd, is a quantum algorithm published in 2008 for solving linear systems. The algorithm estimates the result of a scalar measurement on the solution vector to a given linear system of equations.
The five-qubit error correcting code is the smallest quantum error correcting code that can protect a logical qubit from any arbitrary single qubit error. In this code, 5 physical qubits are used to encode the logical qubit. With and being Pauli matrices and the Identity matrix, this code's generators are . Its logical operators are and . Once the logical qubit is encoded, errors on the physical qubits can be detected via stabilizer measurements. A lookup table that maps the results of the stabilizer measurements to the types and locations of the errors gives the control system of the quantum computer enough information to correct errors.
The Bacon–Shor code is a Subsystem error correcting code. In a Subsystem code, information is encoded in a subsystem of a Hilbert space. Subsystem codes lend to simplified error correcting procedures unlike codes which encode information in the subspace of a Hilbert space. This simplicity led to the first demonstration of fault tolerant circuits on a quantum computer.
This glossary of quantum computing is a list of definitions of terms and concepts used in quantum computing, its sub-disciplines, and related fields.



















