
A quantum computer is a computer that exploits quantum mechanical phenomena. At small scales, physical matter exhibits properties of both particles and waves, and quantum computing leverages this behavior using specialized hardware. Classical physics cannot explain the operation of these quantum devices, and a scalable quantum computer could perform some calculations exponentially faster than any modern "classical" computer. In particular, a large-scale quantum computer could break widely used encryption schemes and aid physicists in performing physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications.
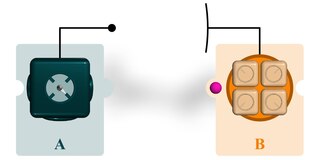
Quantum teleportation is a technique for transferring quantum information from a sender at one location to a receiver some distance away. While teleportation is commonly portrayed in science fiction as a means to transfer physical objects from one location to the next, quantum teleportation only transfers quantum information. The sender does not have to know the particular quantum state being transferred. Moreover, the location of the recipient can be unknown, but to complete the quantum teleportation, classical information needs to be sent from sender to receiver. Because classical information needs to be sent, quantum teleportation cannot occur faster than the speed of light.
In quantum computing, a qubit or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state quantum-mechanical system, one of the simplest quantum systems displaying the peculiarity of quantum mechanics. Examples include the spin of the electron in which the two levels can be taken as spin up and spin down; or the polarization of a single photon in which the two states can be taken to be the vertical polarization and the horizontal polarization. In a classical system, a bit would have to be in one state or the other. However, quantum mechanics allows the qubit to be in a coherent superposition of both states simultaneously, a property that is fundamental to quantum mechanics and quantum computing.
This is a timeline of quantum computing.
Quantum error correction (QEC) is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is theorised as essential to achieve fault tolerant quantum computing that can reduce the effects of noise on stored quantum information, faulty quantum gates, faulty quantum preparation, and faulty measurements. This would allow algorithms of greater circuit depth.

In quantum computing, a charge qubit is a qubit whose basis states are charge states. In superconducting quantum computing, a charge qubit is formed by a tiny superconducting island coupled by a Josephson junction to a superconducting reservoir. The state of the qubit is determined by the number of Cooper pairs that have tunneled across the junction. In contrast with the charge state of an atomic or molecular ion, the charge states of such an "island" involve a macroscopic number of conduction electrons of the island. The quantum superposition of charge states can be achieved by tuning the gate voltage U that controls the chemical potential of the island. The charge qubit is typically read-out by electrostatically coupling the island to an extremely sensitive electrometer such as the radio-frequency single-electron transistor.
Resolved sideband cooling is a laser cooling technique allowing cooling of tightly bound atoms and ions beyond the Doppler cooling limit, potentially to their motional ground state. Aside from the curiosity of having a particle at zero point energy, such preparation of a particle in a definite state with high probability (initialization) is an essential part of state manipulation experiments in quantum optics and quantum computing.

An ion trap is a combination of electric and/or magnetic fields used to capture charged particles — known as ions — often in a system isolated from an external environment. Atomic and molecular ion traps have a number of applications in physics and chemistry such as precision mass spectrometry, improved atomic frequency standards, and quantum computing. In comparison to neutral atom traps, ion traps have deeper trapping potentials that do not depend on the internal electronic structure of a trapped ion. This makes ion traps more suitable for the study of light interactions with single atomic systems. The two most popular types of ion traps are the Penning trap, which forms a potential via a combination of static electric and magnetic fields, and the Paul trap which forms a potential via a combination of static and oscillating electric fields.
Quantum networks form an important element of quantum computing and quantum communication systems. Quantum networks facilitate the transmission of information in the form of quantum bits, also called qubits, between physically separated quantum processors. A quantum processor is a small quantum computer being able to perform quantum logic gates on a certain number of qubits. Quantum networks work in a similar way to classical networks. The main difference is that quantum networking, like quantum computing, is better at solving certain problems, such as modeling quantum systems.

In computer science, the controlled NOT gate, controlled-X gate, controlled-bit-flip gate, Feynman gate or controlled Pauli-X is a quantum logic gate that is an essential component in the construction of a gate-based quantum computer. It can be used to entangle and disentangle Bell states. Any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit rotations. The gate is sometimes named after Richard Feynman who developed an early notation for quantum gate diagrams in 1986.

Nuclear magnetic resonance quantum computing (NMRQC) is one of the several proposed approaches for constructing a quantum computer, that uses the spin states of nuclei within molecules as qubits. The quantum states are probed through the nuclear magnetic resonances, allowing the system to be implemented as a variation of nuclear magnetic resonance spectroscopy. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems, in this case molecules, rather than a single pure state.
A quantum bus is a device which can be used to store or transfer information between independent qubits in a quantum computer, or combine two qubits into a superposition. It is the quantum analog of a classical bus.
In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster C is a connected subset of a d-dimensional lattice, and a cluster state is a pure state of the qubits located on C. They are different from other types of entangled states such as GHZ states or W states in that it is more difficult to eliminate quantum entanglement in the case of cluster states. Another way of thinking of cluster states is as a particular instance of graph states, where the underlying graph is a connected subset of a d-dimensional lattice. Cluster states are especially useful in the context of the one-way quantum computer. For a comprehensible introduction to the topic see.
In quantum mechanics, the cat state, named after Schrödinger's cat, is a quantum state composed of two diametrically opposed conditions at the same time, such as the possibilities that a cat is alive and dead at the same time.

Christopher Roy Monroe is an American physicist and engineer in the areas of atomic, molecular, and optical physics and quantum information science, especially quantum computing. He directs one of the leading research and development efforts in ion trap quantum computing. Monroe is the Gilhuly Family Presidential Distinguished Professor of Electrical and Computer Engineering and Physics at Duke University and is College Park Professor of Physics at the University of Maryland and Fellow of the Joint Quantum Institute and Joint Center for Quantum Computer Science. He is also co-founder and Chief Scientist at IonQ, Inc.
The DiVincenzo criteria are conditions necessary for constructing a quantum computer, conditions proposed in 2000 by the theoretical physicist David P. DiVincenzo, as being those necessary to construct such a computer—a computer first proposed by mathematician Yuri Manin, in 1980, and physicist Richard Feynman, in 1982—as a means to efficiently simulate quantum systems, such as in solving the quantum many-body problem.
The Cirac–Zoller controlled-NOT gate is an implementation of the controlled-NOT (CNOT) quantum logic gate using cold trapped ions that was proposed by Ignacio Cirac and Peter Zoller in 1995 and represents the central ingredient of the Cirac–Zoller proposal for a trapped-ion quantum computer. The key idea of the Cirac–Zoller proposal is to mediate the interaction between the two qubits through the joint motion of the complete chain of trapped ions.

In quantum computing, Mølmer–Sørensen gate scheme refers to an implementation procedure for various multi-qubit quantum logic gates used mostly in trapped ion quantum computing. This procedure is based on the original proposition by Klaus Mølmer and Anders Sørensen in 1999-2000.
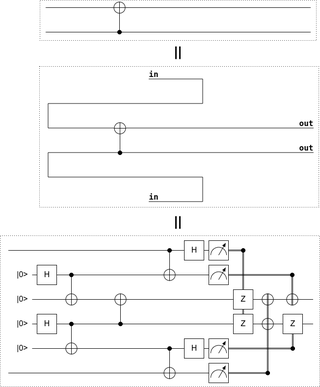
Quantum gate teleportation is a quantum circuit construction where a gate is applied to target qubits by first applying the gate to an entangled state and then teleporting the target qubits through that entangled state.
Quantum logic spectroscopy (QLS) is an ion control scheme that maps quantum information between two co-trapped ion species. Quantum logic operations allow desirable properties of each ion species to be utilized simultaneously. This enables work with ions and molecular ions that have complex internal energy level structures which preclude laser cooling and manipulation of state. QLS was first demonstrated by NIST in 2005. The first QLS of a molecular ion was demonstrated by NIST in 2017.




























