Standard algorithms

Last updated

In elementary arithmetic, a standard algorithm or method is a specific method of computation which is conventionally taught for solving particular mathematical problems. These methods vary somewhat by nation and time, but generally include exchanging, regrouping, long division, and long multiplication using a standard notation, and standard formulas for average, area, and volume. Similar methods also exist for procedures such as square root and even more sophisticated functions, but have fallen out of the general mathematics curriculum in favor of calculators (or tables and slide rules before them). As to standard algorithms in elementary mathematics, Fischer et al. (2019 [1] ) state that advanced students use standard algorithms more effectively than peers who use these algorithms unreasoningly (Fischer et al. [1] 2019). That said, standard algorithms, such as addition, subtraction, as well as those mentioned above, represent central components of elementary math.

Contents

Traditional standard algorithms

Illustration of Traditional Standard Algorithms - Addition, Subtraction, Multiplication, Division Drawing elementary arithmetic standard algorithms.jpg
Illustration of Traditional Standard Algorithms - Addition, Subtraction, Multiplication, Division

Standard algorithms are digit oriented, largely right-handed (begin operations with digits in the ones place), and focus on rules (Charles, [2] 2020). Below, the standard arithmetic algorithms for addition, subtraction, multiplication, and division are described.

Standard addition algorithm

For example, through the standard addition algorithm, the sum can be obtained by following three rules: a) line up the digits of each addend by place value, longer digit addends should go on top, b) each addend can be decomposed -- ones are added with ones, tens are added with tens, and so on, and c) if the sum of the digits of the current place value is ten or greater, then the number must be regrouped.

Standard subtraction algorithm

For the standard subtraction algorithm, the first number is called the minuend and the second number is called the subtrahend. Regarding the rules of this algorithm, the place values of the numbers must align. Then, it must be evaluated whether regrouping or ungrouping is necessary. Then,

either treat each place value column separately and ungroup and subtract before moving on, or check all potential ungroupings first and then perform all the subtractions. (Achieve The Core, nd)

Standard subtraction algorithm. Regrouping and ungrouping. Standard subtraction algorithm (1).jpg
Standard subtraction algorithm. Regrouping and ungrouping.

Standard multiplication algorithm

The main rules for the standard multiplication algorithm of whole numbers follow. In this multiplication procedure, "multiply the multiplicand by each digit of the multiplier and then add up all the appropriately shifted results". (West, [3] 2011) To utilize this method, it is necessary to know the basic multiplication table from zero to nine. (West [3] 2011)

Standard division algorithm

Unlike the other standard algorithms, the division algorithm begins with the larger (left-hand) place values (Lee [4] 2007). The quotient (rounded down to the nearest integer) becomes the first digit of the result. In this process, a maximum digit approaches the virtual product (Leung, [5] 2006), which must be less than the dividend's leading place values. In turn, the difference between the leading place values and the virtual product, or remainder, pushes forward when the process is repeated on the following digit of the dividend ('pulling down' the next digit to the remainder) (Leung, [5] 2006). When all digits have been processed and no remainder is left or the remainder is less than the divisor, the division is complete.

Reform mathematics and standard algorithms in schools

The concepts of reform mathematics which the NCTM introduced in 1989 favors an alternative approach. It proposes a deeper understanding of the underlying theory instead of memorization of specific methods will allow students to develop individual methods which solve the same problems. Students' alternative algorithms are often just as correct, efficient, and generalizable as the standard algorithms, and maintain emphasis on the meaning of the quantities involved, especially as relates to place values (something that is usually lost in the memorization of standard algorithms). The development of sophisticated calculators has made manual calculation less important (see the note on square roots, above) and cursory teaching of traditional methods has created failure among many students. Greater achievement among all types of students is among the primary goals of mathematics education put forth by NCTM. Some researchers such as Constance Kamii have suggested that elementary arithmetic, as traditionally taught, is not appropriate in elementary school. Many first editions of textbooks written to the original 1989 standard such as TERC deliberately discouraged teaching of any particular method, instead devoting class and homework time to the solving of nontrivial problems, which stimulate students to develop their own methods of calculation, rooted in number sense and place value. This emphasis by no means excludes the learning of number facts; indeed, a major goal of early mathematical education is procedural fluency.

The NCTM in recent revisions has made more explicit this need for learning of basic math facts and correct, efficient methods. Many new editions of standards-based texts do present standard methods and basic skills. However, the original guidelines continue to draw fire from well-meaning parents and community members, some of whom advocate a return to traditional mathematics. Success of a particular text depends not only upon its content, but also on the willingness of a school community to allow new pedagogy and content and to commit to the recommended implementation of the materials.

Related Research Articles

<span class="mw-page-title-main">Arithmetic</span> Branch of elementary mathematics

Arithmetic is an elementary branch of mathematics that studies numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms. Arithmetic systems can be distinguished based on the type of number they operate on. Integer arithmetic restricts itself to calculations with positive and negative whole numbers. Rational number arithmetic involves operations on fractions that lie between integers. Real number arithmetic includes calculations with both rational and irrational numbers and covers the complete number line. Another distinction is based on the numeral system employed to perform calculations. Decimal arithmetic is the most common. It uses the basic numerals from 0 to 9 and their combinations to express numbers. Binary arithmetic, by contrast, is used by most computers and represents numbers as combinations of the basic numerals 0 and 1. Some arithmetic systems operate on mathematical objects other than numbers, such as interval arithmetic and matrix arithmetic.

<span class="mw-page-title-main">Modular arithmetic</span> Computation modulo a fixed integer

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.

<span class="mw-page-title-main">Division (mathematics)</span> Arithmetic operation

Division is one of the four basic operations of arithmetic. The other operations are addition, subtraction, and multiplication. What is being divided is called the dividend, which is divided by the divisor, and the result is called the quotient.

<span class="mw-page-title-main">Multiplication table</span> Mathematical table

In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system.

<span class="mw-page-title-main">Addition</span> Arithmetic operation

Addition is one of the four basic operations of arithmetic, the other three being subtraction, multiplication and division. The addition of two whole numbers results in the total amount or sum of those values combined. The example in the adjacent image shows two columns of three apples and two apples each, totaling at five apples. This observation is equivalent to the mathematical expression "3 + 2 = 5".

<span class="mw-page-title-main">Subtraction</span> One of the four basic arithmetic operations

Subtraction is one of the four arithmetic operations along with addition, multiplication and division. Subtraction is an operation that represents removal of objects from a collection. For example, in the adjacent picture, there are 5 − 2 peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches. Therefore, the difference of 5 and 2 is 3; that is, 5 − 2 = 3. While primarily associated with natural numbers in arithmetic, subtraction can also represent removing or decreasing physical and abstract quantities using different kinds of objects including negative numbers, fractions, irrational numbers, vectors, decimals, functions, and matrices.

In mathematics and computer programming, the order of operations is a collection of rules that reflect conventions about which operations to perform first in order to evaluate a given mathematical expression.

In arithmetic, long division is a standard division algorithm suitable for dividing multi-digit Hindu-Arabic numerals that is simple enough to perform by hand. It breaks down a division problem into a series of easier steps.

The soroban is an abacus developed in Japan. It is derived from the ancient Chinese suanpan, imported to Japan in the 14th century. Like the suanpan, the soroban is still used today, despite the proliferation of practical and affordable pocket electronic calculators.

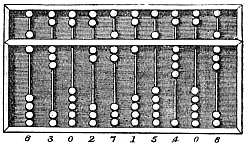
<span class="mw-page-title-main">Suanpan</span> Chinese abacus

The suanpan, also spelled suan pan or souanpan) is an abacus of Chinese origin first described in a 190 CE book of the Eastern Han Dynasty, namely Supplementary Notes on the Art of Figures written by Xu Yue. However, the exact design of this suanpan is not known. Usually, a suanpan is about 20 cm (8 in) tall and it comes in various widths depending on the application. It usually has more than seven rods. There are two beads on each rod in the upper deck and five beads on each rod in the bottom deck. The beads are usually rounded and made of a hardwood. The beads are counted by moving them up or down towards the beam. The suanpan can be reset to the starting position instantly by a quick jerk around the horizontal axis to spin all the beads away from the horizontal beam at the center.

Principles and Standards for School Mathematics (PSSM) are guidelines produced by the National Council of Teachers of Mathematics (NCTM) in 2000, setting forth recommendations for mathematics educators. They form a national vision for preschool through twelfth grade mathematics education in the US and Canada. It is the primary model for standards-based mathematics.

Founded in 1920, The National Council of Teachers of Mathematics (NCTM) is a professional organization for schoolteachers of mathematics in the United States. One of its goals is to improve the standards of mathematics in education. NCTM holds annual national and regional conferences for teachers and publishes five journals.

<span class="mw-page-title-main">Elementary arithmetic</span> Numbers and the basic operations on them

Elementary arithmetic is a branch of mathematics involving basic numerical operations, namely addition, subtraction, multiplication, and division. Due to the low level of abstraction, broad range of application, and position as the foundation of all mathematics, elementary arithmetic is generally known as the first branch of mathematics mainly taught in elementary/primary school.

A division algorithm is an algorithm which, given two integers N and D, computes their quotient and/or remainder, the result of Euclidean division. Some are applied by hand, while others are employed by digital circuit designs and software.

Traditional mathematics was the predominant method of mathematics education in the United States in the early-to-mid 20th century. This contrasts with non-traditional approaches to math education. Traditional mathematics education has been challenged by several reform movements over the last several decades, notably new math, a now largely abandoned and discredited set of alternative methods, and most recently reform or standards-based mathematics based on NCTM standards, which is federally supported and has been widely adopted, but subject to ongoing criticism.

Investigations in Numbers, Data, and Space is a K–5 mathematics curriculum, developed at TERC in Cambridge, Massachusetts, United States. The curriculum is often referred to as Investigations or simply TERC. Patterned after the NCTM standards for mathematics, it is among the most widely used of the new reform mathematics curricula. As opposed to referring to textbooks and having teachers impose methods for solving arithmetic problems, the TERC program uses a constructivist approach that encourages students to develop their own understanding of mathematics. The curriculum underwent a major revision in 2005–2007.

MathLand was one of several elementary mathematics curricula that were designed around the 1989 NCTM standards. It was developed and published by Creative Publications and was initially adopted by the U.S. state of California and schools run by the US Department of Defense by the mid 1990s. Unlike curricula such as Investigations in Numbers, Data, and Space, by 2007 Mathland was no longer offered by the publisher, and has since been dropped by many early adopters. Its demise may have been, at least in part, a result of intense scrutiny by critics.

Math wars is the debate over modern mathematics education, textbooks and curricula in the United States that was triggered by the publication in 1989 of the Curriculum and Evaluation Standards for School Mathematics by the National Council of Teachers of Mathematics (NCTM) and subsequent development and widespread adoption of a new generation of mathematics curricula inspired by these standards.

Reform mathematics is an approach to mathematics education, particularly in North America. It is based on principles explained in 1989 by the National Council of Teachers of Mathematics (NCTM). The NCTM document Curriculum and Evaluation Standards for School Mathematics (CESSM) set forth a vision for K–12 mathematics education in the United States and Canada. The CESSM recommendations were adopted by many local- and federal-level education agencies during the 1990s. In 2000, the NCTM revised its CESSM with the publication of Principles and Standards for School Mathematics (PSSM). Like those in the first publication, the updated recommendations became the basis for many states' mathematics standards, and the method in textbooks developed by many federally-funded projects. The CESSM de-emphasised manual arithmetic in favor of students developing their own conceptual thinking and problem solving. The PSSM presents a more balanced view, but still has the same emphases.

<i>Principles of Hindu Reckoning</i>

Principles of Hindu Reckoning is a mathematics book written by the 10th- and 11th-century Persian mathematician Kushyar ibn Labban. It is the second-oldest book extant in Arabic about Hindu arithmetic using Hindu-Arabic numerals, preceded by Kibab al-Fusul fi al-Hisub al-Hindi by Abul al-Hassan Ahmad ibn Ibrahim al-Uglidis, written in 952.

References

  1. 1 2 Fischer, Jean-Paul; Vilette, Bruno; Joffredo-Lebrun, Sophie; Morellato, Mireille; Le Normand, Céline; Scheibling-Seve, Calliste; Richard, Jean-François (2019-05-01). "Should we continue to teach standard written algorithms for the arithmetical operations? The example of subtraction". Educational Studies in Mathematics. 101 (1): 105–121. doi:10.1007/s10649-019-09884-9. ISSN   1573-0816. S2CID   254476042.
  2. ↑ Charles, R. I. (2020). A New Vision for Developing Addition and Subtraction Computation Strategies. Pearson Education.{{cite book}}: CS1 maint: date and year (link)
  3. 1 2 West, L., & Bellevue, N. E. (2011). An introduction to various multiplication strategies. Washington. USA. Merrill Prentice Hall.
  4. ↑ Lee, Ji-Eun (2007-01-01). "Making sense of the traditional long division algorithm". The Journal of Mathematical Behavior. 26 (1): 48–59. doi:10.1016/j.jmathb.2007.03.001. ISSN   0732-3123.
  5. 1 2 LEUNG, K. C. I., Wong, R. M., & PANG, W. S. (2006). Departing from the traditional long division algorithm: An experimental study.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.