
In geometry, any polyhedron is associated with a second dual figure, where the vertices of one correspond to the faces of the other and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all are also geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

A fullerene is an allotrope of carbon whose molecule consists of carbon atoms connected by single and double bonds so as to form a closed or partially closed mesh, with fused rings of five to seven atoms. The molecule may be a hollow sphere, ellipsoid, tube, or many other shapes and sizes. Graphene, which is a flat mesh of regular hexagonal rings, can be seen as an extreme member of the family.

In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- + -hedron.
In three-dimensional space, a Platonic solid is a regular, convex polyhedron. It is constructed by congruent, regular, polygonal faces with the same number of faces meeting at each vertex. Five solids meet these criteria:
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.
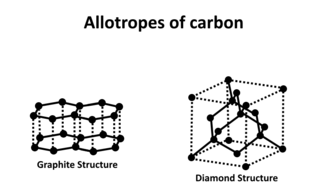
Carbon is capable of forming many allotropes due to its valency. Well-known forms of carbon include diamond and graphite. In recent decades, many more allotropes have been discovered and researched including ball shapes such as buckminsterfullerene and sheets such as graphene. Larger scale structures of carbon include nanotubes, nanobuds and nanoribbons. Other unusual forms of carbon exist at very high temperatures or extreme pressures. Around 500 hypothetical 3-periodic allotropes of carbon are known at the present time, according to the Samara Carbon Allotrope Database (SACADA).

In geometry, a pentakis dodecahedron or kisdodecahedron is the polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. It is a Catalan Solid, meaning that it is a dual of an Archimedean Solid, in this case, the Truncated Icosahedron.
In chemistry the polyhedral skeletal electron pair theory (PSEPT) provides electron counting rules useful for predicting the structures of clusters such as borane and carborane clusters. The electron counting rules were originally formulated by Kenneth Wade and were further developed by Michael Mingos and others; they are sometimes known as Wade's rules or the Wade–Mingos rules. The rules are based on a molecular orbital treatment of the bonding. These rules have been extended and unified in the form of the Jemmis mno rules.

A Stone–Wales defect is a crystallographic defect that involves the change of connectivity of two π-bonded carbon atoms, leading to their rotation by 90° with respect to the midpoint of their bond. The reaction commonly involves conversion between a naphthalene-like structure into a fulvalene-like structure, that is, two rings that share an edge vs two separate rings that have vertices bonded to each other.

In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.

CoNTub is a software project written in Java which runs on Windows, Mac OS X, Linux and Unix Operating systems through any Java-enabled web browser. It is the first implementation of an algorithm for generating 3D structures of arbitrary carbon nanotube connections by means of the placement of non-hexagonal rings, also referred as defects or disclinations.
The mechanical properties of carbon nanotubes reveal them as one of the strongest materials in nature. Carbon nanotubes (CNTs) are long hollow cylinders of graphene. Although graphene sheets have 2D symmetry, carbon nanotubes by geometry have different properties in axial and radial directions. It has been shown that CNTs are very strong in the axial direction. Young's modulus on the order of 270 - 950 GPa and tensile strength of 11 - 63 GPa were obtained.

Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same number of vertices, edges and faces as the regular icosahedron. It is named for Børge Jessen who studied it in 1967, although the same shape had also been constructed earlier by Kenneth Snelson.
The Alexandrov uniqueness theorem is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between points on their surfaces. It implies that convex polyhedra with distinct shapes from each other also have distinct metric spaces of surface distances, and it characterizes the metric spaces that come from the surface distances on polyhedra. It is named after Soviet mathematician Aleksandr Danilovich Aleksandrov, who published it in the 1940s.

In geometry, the density of a star polyhedron is a generalization of the concept of winding number from two dimensions to higher dimensions, representing the number of windings of the polyhedron around the center of symmetry of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the facets of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed facets.

In geometry and crystallography, the Laves graph is an infinite cubic symmetric graph. It can be embedded into three-dimensional space, with integer coordinates, to form a structure with chiral symmetry in which the three edges at each vertex form 120° angles to each other. It can also be defined more abstractly as a covering graph of the complete graph on four vertices.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.














