
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance of one or more quantities. Periodic waves oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero.

The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics.

Longitudinal waves are waves which oscillate in the direction which is parallel to the direction in which the wave travels and displacement of the medium is in the same direction of the wave propagation. Mechanical longitudinal waves are also called compressional or compression waves, because they produce compression and rarefaction when travelling through a medium, and pressure waves, because they produce increases and decreases in pressure. A wave along the length of a stretched Slinky toy, where the distance between coils increases and decreases, is a good visualization. Real-world examples include sound waves and seismic P waves.

The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. More simply, the speed of sound is how fast vibrations travel. At 20 °C (68 °F), the speed of sound in air, is about 343 m/s, or 1 km in 2.91 s or one mile in 4.69 s. It depends strongly on temperature as well as the medium through which a sound wave is propagating.
Linear elasticity is a mathematical model as to how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.

Shear stress is the component of stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. Normal stress, on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts.
Particle velocity is the velocity of a particle in a medium as it transmits a wave. The SI unit of particle velocity is the metre per second (m/s). In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string.
Acoustic impedance and specific acoustic impedance are measures of the opposition that a system presents to the acoustic flow resulting from an acoustic pressure applied to the system. The SI unit of acoustic impedance is the pascal-second per cubic metre, or in the MKS system the rayl per square metre (Rayl/m2), while that of specific acoustic impedance is the pascal-second per metre (Pa·s/m), or in the MKS system the rayl (Rayl). There is a close analogy with electrical impedance, which measures the opposition that a system presents to the electric current resulting from a voltage applied to the system.

In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves are a type of elastic wave and are one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves.

Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects.
In physics, the acoustic wave equation is a second-order partial differential equation that governs the propagation of acoustic waves through a material medium resp. a standing wavefield. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position x and time t. A simplified (scalar) form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions.

Poromechanics is a branch of physics and specifically continuum mechanics that studies the behavior of fluid-saturated porous media. A porous medium or a porous material is a solid, constituting the matrix, which is permeated by an interconnected network of pores or voids filled with a fluid. In general, the fluid may be composed of liquid or gas phases or both. In the simplest case, both the solid matrix and the pore space constitute two separate, continuously connected domains. An archtypal example of such a porous material is the kitchen sponge, which is formed of two interpenetrating continua. Some porous media has a more complex microstructure in which, for example, the porespace is disconnected. Porespace that is unable to exchange fluid with the exterior is termed occluded porespace. Alternatively, in the case of granular porous media, the solid phase may constitute disconnected domains, termed the "grains", which are load-bearing under compression, though can flow when sheared.
Computational aeroacoustics is a branch of aeroacoustics that aims to analyze the generation of noise by turbulent flows through numerical methods.
Acoustic waves are disturbances that propagate through a medium—such as air, water, or solids—by causing the particles of the medium to compress and expand. These waves carry energy and are characterized by properties like acoustic pressure, particle velocity, and acoustic intensity. The speed of an acoustic wave depends on the properties of the medium it travels through; for example, it travels at approximately 343 meters per second in air, and 1480 meters per second in water. Acoustic waves encompass a broad range of phenomena, from audible sound to seismic waves and ultrasound, finding applications in diverse fields like acoustics, engineering, and medicine.
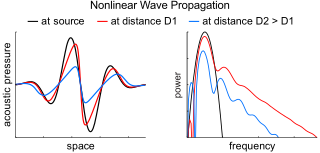
Nonlinear acoustics (NLA) is a branch of physics and acoustics dealing with sound waves of sufficiently large amplitudes. Large amplitudes require using full systems of governing equations of fluid dynamics and elasticity. These equations are generally nonlinear, and their traditional linearization is no longer possible. The solutions of these equations show that, due to the effects of nonlinearity, sound waves are being distorted as they travel.
An acoustic rheometer is a device used to measure the rheological properties of fluids, such as viscosity and elasticity, by utilizing sound waves. It works by generating acoustic waves in the fluid and analyzing the changes in the wave propagation caused by the fluid's rheological behavior. An acoustic rheometer uses a piezo-electric crystal to generate the acoustic waves, applying an oscillating extensional stress to the system. System response can be interpreted in terms of extensional rheology.
Acoustic streaming is a steady flow in a fluid driven by the absorption of high amplitude acoustic oscillations. This phenomenon can be observed near sound emitters, or in the standing waves within a Kundt's tube. Acoustic streaming was explained first by Lord Rayleigh in 1884. It is the less-known opposite of sound generation by a flow.

In numerical analysis, the interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics, composite structures, biomechanics and in many other areas. The goal of the Interval Finite Element is to find upper and lower bounds of different characteristics of the model and use these results in the design process. This is so called worst case design, which is closely related to the limit state design.
The acoustoelastic effect is how the sound velocities of an elastic material change if subjected to an initial static stress field. This is a non-linear effect of the constitutive relation between mechanical stress and finite strain in a material of continuous mass. In classical linear elasticity theory small deformations of most elastic materials can be described by a linear relation between the applied stress and the resulting strain. This relationship is commonly known as the generalised Hooke's law. The linear elastic theory involves second order elastic constants and yields constant longitudinal and shear sound velocities in an elastic material, not affected by an applied stress. The acoustoelastic effect on the other hand include higher order expansion of the constitutive relation between the applied stress and resulting strain, which yields longitudinal and shear sound velocities dependent of the stress state of the material. In the limit of an unstressed material the sound velocities of the linear elastic theory are reproduced.



















