
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation for an arbitrary complex number , which represents the order of the Bessel function. Although and produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of .

In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field.

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.
In mathematics, de Moivre's formula states that for any real number x and integer n it is the case that where i is the imaginary unit. The formula is named after Abraham de Moivre, although he never stated it in his works. The expression cos x + i sin x is sometimes abbreviated to cis x.

In mathematics, Legendre polynomials, named after Adrien-Marie Legendre (1782), are a system of complete and orthogonal polynomials with a wide number of mathematical properties and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.

In mathematics, a trigonometric substitution replaces a trigonometric function for another expression. In calculus, trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.

In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
In mathematics, Mathieu functions, sometimes called angular Mathieu functions, are solutions of Mathieu's differential equation
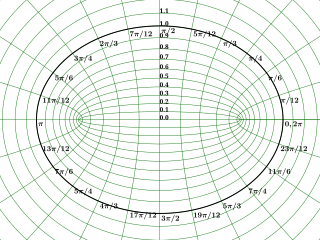
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci and are generally taken to be fixed at and , respectively, on the -axis of the Cartesian coordinate system.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
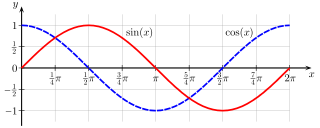
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted as and .

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
In hyperbolic geometry, the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from plane trigonometry, or the spherical law of cosines in spherical trigonometry. It can also be related to the relativistic velocity addition formula.
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force.





























