
The spider and the fly problem is a recreational mathematics problem with an unintuitive solution, asking for a shortest path or geodesic between two points on the surface of a cuboid. It was originally posed by Henry Dudeney.

The spider and the fly problem is a recreational mathematics problem with an unintuitive solution, asking for a shortest path or geodesic between two points on the surface of a cuboid. It was originally posed by Henry Dudeney.
In the typical version of the puzzle, an otherwise empty cuboid room 30 feet long, 12 feet wide and 12 feet high contains a spider and a fly. The spider is 1 foot below the ceiling and horizontally centred on one 12′×12′ wall. The fly is 1 foot above the floor and horizontally centred on the opposite wall. The problem is to find the minimum distance the spider must crawl along the walls, ceiling and/or floor to reach the fly, which remains stationary. [1]
A naive solution is for the spider to remain horizontally centred, and crawl up to the ceiling, across it and down to the fly, giving a distance of 42 feet. Instead, the shortest path, 40 feet long, spirals around five of the six faces of the cuboid. Alternatively, it can be described by unfolding the cuboid into a net and finding a shortest path (a line segment) on the resulting unfolded system of six rectangles in the plane. Different nets produce different segments with different lengths, and the question becomes one of finding a net whose segment length is minimum. [2] Another path, of intermediate length , crosses diagonally through four faces instead of five. [3]
For a room of length l, width w and height h, the spider a distance b below the ceiling, and the fly a distance a above the floor, length of the spiral path is while the naive solution has length . [1] Depending on the dimensions of the cuboid, and on the initial positions of the spider and fly, one or another of these paths, or of four other paths, may be the optimal solution. [4] However, there is no rectangular cuboid, and two points on the cuboid, for which the shortest path passes through all six faces of the cuboid. [5]
A different lateral thinking solution, beyond the stated rules of the puzzle, involves the spider attaching dragline silk to the wall to lower itself to the floor, and crawling 30 feet across it and 1 foot up the opposite wall, giving a crawl distance of 31 feet. Similarly, it can climb to the ceiling, cross it, then attach the silk to lower itself 11 feet, also a 31-foot crawl. [6]
The problem was originally posed by Henry Dudeney in the English newspaper Weekly Dispatch on 14 June 1903 and collected in The Canterbury Puzzles (1907). Martin Gardner calls it "Dudeney's best-known brain-teaser". [7]
A version of the problem was recorded by Adolf Hurwitz in his diary in 1908. Hurwitz stated that he heard it from L. Gustave du Pasquier, who in turn had heard it from Richard von Mises. [8]
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system the base unit for length is the metre.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

The Tower of Hanoi is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical shape. The objective of the puzzle is to move the entire stack to one of the other rods, obeying the following rules:
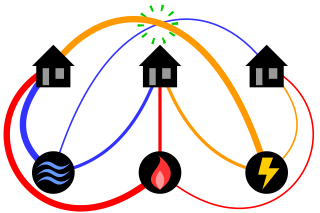
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.

In geometry, a geodesic is a curve representing in some sense the shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line".

Dynamic programming is both a mathematical optimization method and an algorithmic paradigm. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In physics and mathematics, a brachistochrone curve, or curve of fastest descent, is the one lying on the plane between a point A and a lower point B, where B is not directly below A, on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696.

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance or shortest-path distance. Notice that there may be more than one shortest path between two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite.

In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard.
In mathematics, an Euler brick, named after Leonhard Euler, is a rectangular cuboid whose edges and face diagonals all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime. A perfect Euler brick is one whose space diagonal is also an integer, but such a brick has not yet been found.
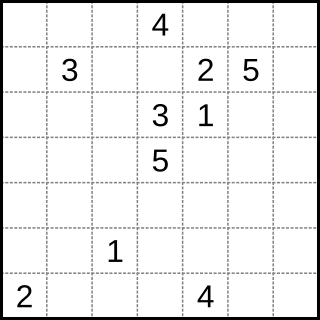
Numberlink is a type of logic puzzle involving finding paths to connect numbers in a grid.
The crossed ladders problem is a puzzle of unknown origin that has appeared in various publications and regularly reappears in Web pages and Usenet discussions.

The nine dots puzzle is a mathematical puzzle whose task is to connect nine squarely arranged points with a pen by four straight lines without lifting the pen.

An edge-matching puzzle is a type of tiling puzzle involving tiling an area with polygons whose edges are distinguished with colours or patterns, in such a way that the edges of adjacent tiles match.

In geometry, a hinged dissection, also known as a swing-hinged dissection or Dudeney dissection, is a kind of geometric dissection in which all of the pieces are connected into a chain by "hinged" points, such that the rearrangement from one figure to another can be carried out by swinging the chain continuously, without severing any of the connections. Typically, it is assumed that the pieces are allowed to overlap in the folding and unfolding process; this is sometimes called the "wobbly-hinged" model of hinged dissection.
In differential geometry the theorem of the three geodesics, also known as Lyusternik–Schnirelmann theorem, states that every Riemannian manifold with the topology of a sphere has at least three simple closed geodesics. The result can also be extended to quasigeodesics on a convex polyhedron, and to closed geodesics of reversible Finsler 2-spheres. The theorem is sharp: although every Riemannian 2-sphere contains infinitely many distinct closed geodesics, only three of them are guaranteed to have no self-intersections. For example, by a result of Morse if the lengths of three principal axes of an ellipsoid are distinct, but sufficiently close to each other, then the ellipsoid has only three simple closed geodesics.
In discrete mathematics and theoretical computer science, reconfiguration problems are computational problems involving reachability or connectivity of state spaces.