The Nash embedding theorems, named after John Forbes Nash Jr., state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path. For instance, bending but neither stretching nor tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
In the mathematical field of differential geometry, the Gauss–Bonnet theorem is a fundamental formula which links the curvature of a surface to its underlying topology.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
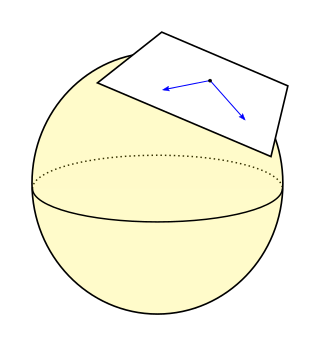
In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a smooth surface in three-dimensional space at a point is the product of the principal curvatures, κ1 and κ2, at the given point:
Richard Streit Hamilton is an American mathematician who serves as the Davies Professor of Mathematics at Columbia University. He is known for contributions to geometric analysis and partial differential equations. Hamilton is best known for foundational contributions to the theory of the Ricci flow and the development of a corresponding program of techniques and ideas for resolving the Poincaré conjecture and geometrization conjecture in the field of geometric topology. Grigori Perelman built upon Hamilton's results to prove the conjectures, and was awarded a Millennium Prize for his work. However, Perelman declined the award, regarding Hamilton's contribution as being equal to his own.
In differential geometry, Fenchel's theorem is an inequality on the total absolute curvature of a closed smooth space curve, stating that it is always at least . Equivalently, the average curvature is at least , where is the length of the curve. The only curves of this type whose total absolute curvature equals and whose average curvature equals are the plane convex curves. The theorem is named after Werner Fenchel, who published it in 1929.
In the mathematical theory of knots, the Fáry–Milnor theorem, named after István Fáry and John Milnor, states that three-dimensional smooth curves with small total curvature must be unknotted. The theorem was proved independently by Fáry in 1949 and Milnor in 1950. It was later shown to follow from the existence of quadrisecants.
The four-vertex theorem of geometry states that the curvature along a simple, closed, smooth plane curve has at least four local extrema. The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex. This theorem has many generalizations, including a version for space curves where a vertex is defined as a point of vanishing torsion.
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arc length:
The Alexandrov uniqueness theorem is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between points on their surfaces. It implies that convex polyhedra with distinct shapes from each other also have distinct metric spaces of surface distances, and it characterizes the metric spaces that come from the surface distances on polyhedra. It is named after Soviet mathematician Aleksandr Danilovich Aleksandrov, who published it in the 1940s.
In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.
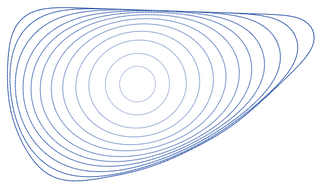
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.
Shi Yuguang is a Chinese mathematician at Peking University. His areas of research are geometric analysis and differential geometry.
In differential geometry the theorem of the three geodesics, also known as Lyusternik–Schnirelmann theorem, states that every Riemannian manifold with the topology of a sphere has at least three simple closed geodesics. The result can also be extended to quasigeodesics on a convex polyhedron, and to closed geodesics of reversible Finsler 2-spheres. The theorem is sharp: although every Riemannian 2-sphere contains infinitely many distinct closed geodesics, only three of them are guaranteed to have no self-intersections. For example, by a result of Morse if the lengths of three principal axes of an ellipsoid are distinct, but sufficiently close to each other, then the ellipsoid has only three simple closed geodesics.
In differential geometry, the Angenent torus is a smooth embedding of the torus into three-dimensional Euclidean space, with the property that it remains self-similar as it evolves under the mean curvature flow. Its existence shows that, unlike the one-dimensional curve-shortening flow, the two-dimensional mean-curvature flow has embedded surfaces that form more complex singularities as they collapse.
In geometry, the tennis ball theorem states that any smooth curve on the surface of a sphere that divides the sphere into two equal-area subsets without touching or crossing itself must have at least four inflection points, points at which the curve does not consistently bend to only one side of its tangent line. The tennis ball theorem was first published under this name by Vladimir Arnold in 1994, and is often attributed to Arnold, but a closely related result appears earlier in a 1968 paper by Beniamino Segre, and the tennis ball theorem itself is a special case of a theorem in a 1977 paper by Joel L. Weiner. The name of the theorem comes from the standard shape of a tennis ball, whose seam forms a curve that meets the conditions of the theorem; the same kind of curve is also used for the seams on baseballs.
In the mathematical fields of differential geometry and geometric analysis, the Gauss curvature flow is a geometric flow for oriented hypersurfaces of Riemannian manifolds. In the case of curves in a two-dimensional manifold, it is identical with the curve shortening flow. The mean curvature flow is a different geometric flow which also has the curve shortening flow as a special case.
Extrinsic Geometric Flows is an advanced mathematics textbook that overviews geometric flows, mathematical problems in which a curve or surface moves continuously according to some rule. It focuses on extrinsic flows, in which the rule depends on the embedding of a surface into space, rather than intrinsic flows such as the Ricci flow that depend on the internal geometry of the surface and can be defined without respect to an embedding.
