Triangle conic

In Euclidean geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse, which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle; the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle; and the Artzt parabolas, which are parabolas touching two sidelines of the reference triangle at vertices of the triangle.

The terminology of triangle conic is widely used in the literature without a formal definition; that is, without precisely formulating the relations a conic should have with the reference triangle so as to qualify it to be called a triangle conic (see ^{[1] [2] [3] [4]} ). However, Greek mathematician Paris Pamfilos defines a triangle conic as a "conic circumscribing a triangle △ABC (that is, passing through its vertices) or inscribed in a triangle (that is, tangent to its side-lines)". ^{[5] [6]} The terminology triangle circle (respectively, ellipse, hyperbola, parabola ) is used to denote a circle (respectively, ellipse, hyperbola, parabola) associated with the reference triangle is some way.

Even though several triangle conics have been studied individually, there is no comprehensive encyclopedia or catalogue of triangle conics similar to Clark Kimberling's Encyclopedia of Triangle Centres or Bernard Gibert's Catalogue of Triangle Cubics. ^[7]

Equations of triangle conics in trilinear coordinates

The equation of a general triangle conic in trilinear coordinates x : y : z has the form $${\displaystyle rx^{2}+sy^{2}+tz^{2}+2uyz+2vzx+2wxy=0.}$$ The equations of triangle circumconics and inconics have respectively the forms $${\displaystyle {\begin{aligned}&uyz+vzx+wxy=0\\[2pt]&l^{2}x^{2}+m^{2}y^{2}+n^{2}z^{2}-2mnyz-2nlzx-2lmxy=0\end{aligned}}}$$

Dual conics

A circumconic and an inconic are said to be dual if the barycentric coordinates of any point on the circumconic correspond to coefficients of the homogeneous equation of a tangent to the inconic. Pairs of dual conics include the Steiner ellipse and the Steiner inellipse, and the Kiepert hyperbola and the Kiepert parabola.

The perspector of a circumconic or inconic is the perspector of the reference triangle and its polar triangle with respect to the conic. Several properties hold:

• Perspectors of dual conics are isotomic conjugates. ^[8]
• A circumconic may be described as the locus of trilinear poles of lines through its perspector. ^[9] Conversely, the perspector of a nondegenerate circumconic may be found as the intersection of trilinear polars of any two points on the conic other than the vertices of the triangle. ^[10]
• The perspector of an inconic is the same as its Brianchon point. ^[11]
• The dual circumconic of an inconic is the isotomic conjugate of the trilinear polar of the inconic's perspector. ^[12]

Not all conics associated with a triangle are circumconics or inconics; for instance, the Artzt parabolas each only touch two vertices.

Paris Pamfilos describes a different notion of dual conics based on projective transformations of an equilateral triangle, which also includes the Steiner ellipse and inellipse. ^[13]

Special triangle conics

In the following, a few typical special triangle conics are discussed. In the descriptions, the standard notations are used: the reference triangle is always denoted by △ABC. The angles at the vertices A, B, C are denoted by A, B, C and the lengths of the sides opposite to the vertices A, B, C are respectively a, b, c. The equations of the conics are given in the trilinear coordinates x : y : z. The conics are selected as illustrative of the several different ways in which a conic could be associated with a triangle.

Triangle circles

Some well known triangle circles ^[14]

No.	Name	Definition	Equation	Figure
1	Circumcircle	Circle which passes through the vertices	${\displaystyle {\frac {a}{x}}+{\frac {b}{y}}+{\frac {c}{z}}=0}$	Circumcircle of △ABC
2	Incircle	Circle which touches the sidelines internally	${\displaystyle \pm {\sqrt {x}}\cos {\frac {A}{2}}\pm {\sqrt {y}}\cos {\frac {B}{2}}\pm {\sqrt {z}}\cos {\frac {C}{2}}=0}$	Incircle of △ABC
3	Excircles (or escribed circles)	A circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles.	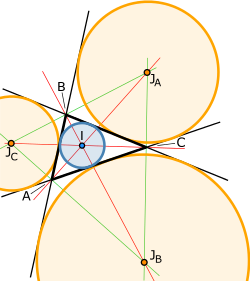${\displaystyle {\begin{aligned}\pm {\sqrt {-x}}\cos {\frac {A}{2}}\pm {\sqrt {y}}\cos {\frac {B}{2}}\pm {\sqrt {z}}\cos {\frac {C}{2}}&=0\\[2pt]\pm {\sqrt {x}}\cos {\frac {A}{2}}\pm {\sqrt {-y}}\cos {\frac {B}{2}}\pm {\sqrt {z}}\cos {\frac {C}{2}}&=0\\[2pt]\pm {\sqrt {x}}\cos {\frac {A}{2}}\pm {\sqrt {y}}\cos {\frac {B}{2}}\pm {\sqrt {-z}}\cos {\frac {C}{2}}&=0\end{aligned}}}$	Incircle and excircles
4	Nine-point circle (or Feuerbach's circle, Euler's circle, Terquem's circle)	Circle passing through the midpoint of the sides, the foot of altitudes and the midpoints of the line segments from each vertex to the orthocenter	${\displaystyle {\begin{aligned}&x^{2}\sin 2A+y^{2}\sin 2B+z^{2}\sin 2C\ -\\&2(yz\sin A+zx\sin B+xy\sin C)=0\end{aligned}}}$	The nine points
5	Orthocentroidal circle	Circle with the line segment joining the orthocenter H to the centroid G as a diameter		Orthocentroidal circle of △ABC with shaded interior
6	Brocard circle	Circle with the line segment joining the symmedian point K to the circumcenter O as a diameter		Brocard circle of △ABC
7	Cosine circle (or second Lemoine circle)	Draw lines through K antiparallel to the sides of △ABC. The six points where the lines intersect the sides lie on a circle known as the cosine circle, as the chord on each side is proportional to the cosine of the opposite angle. Its center is K. The six points form an inscribed hexagon with sides alternately antiparallel and parallel to the sides of △ABC. Such a hexagon is always cyclic and lies on a Tucker circle, of which the cosine circle and circumcircle are special cases. All Tucker circles have center on the line KO (the Brocard axis). [15]		Cosine circle of △ABC
8	First Lemoine circle	Draw lines through K parallel to the sides of △ABC. The six points where the lines intersect the sides lie on a circle known as the first Lemoine circle. It is a Tucker circle and its center is the midpoint of K and O.		First Lemoine circle of △ABC

Triangle ellipses

Some well known triangle ellipses

No.	Name	Definition	Equation	Figure
1	Steiner ellipse	Conic passing through the vertices of △ABC and having centre at the centroid of △ABC	${\displaystyle {\frac {1}{ax}}+{\frac {1}{by}}+{\frac {1}{cz}}=0}$	Steiner ellipse of △ABC
2	Steiner inellipse	Ellipse touching the sidelines at the midpoints of the sides	${\displaystyle {\begin{aligned}&a^{2}x^{2}+b^{2}y^{2}+c^{2}z^{2}-\\&2bcyz-2cazx-2abxy=0\end{aligned}}}$	Steiner inellipse of △ABC
3	Mandart inellipse	Ellipse touching the sidelines at the contact points of the excircles. Its center is the mittenpunkt and its perspector is the Nagel point.	${\displaystyle {\begin{aligned}&f^{2}x^{2}+g^{2}y^{2}+h^{2}z^{2}-\\[2pt]&2fgxy-2ghyz-2hfxz=0,\\[8pt]&{\text{where }}f={\frac {a}{b+c-a}},\\&g={\frac {b}{a+c-b}},\ h={\frac {c}{a+b-c}}.\end{aligned}}}$	Mandart inellipse of △ABC

Triangle hyperbolas

Some well known triangle hyperbolas

No.	Name	Definition	Equation	Figure
1	Kiepert hyperbola [10]	If the three triangles △XBC, △YCA, △ZAB, constructed on the sides of △ABC as bases, are similar, isosceles and similarly situated, then the lines AX, BY, CZ concur at a point N. The locus of N is the Kiepert hyperbola. The Kiepert hyperbola is rectangular and passes through the orthocenter and the centroid of △ABC. It is the isotomic conjugate of ${\displaystyle GK}$, the line joining the centroid and the symmedian point, and the isogonal conjugate of the Brocard axis. Its center, the orthopole of the Brocard axis, is the Steiner point of the medial triangle, and lies on the nine-point circle and the Steiner inellipse. Its perspector is the intersection of the orthic axis and the line at infinity.	${\displaystyle {\frac {\sin(B-C)}{x}}+{\frac {\sin(C-A)}{y}}+{\frac {\sin(A-B)}{z}}=0}$	Kiepert hyperbola of △ABC. The hyperbola passes through the vertices A, B, C, the orthocenter (O) and the centroid (G) of the triangle.
2	Jerabek hyperbola [10]	Rectangular hyperbola passing through the vertices, the orthocenter and the circumcenter of △ABC. Isogonal conjugate of the Euler line. Its center, the orthopole of the Euler line, is the focus of the Kiepert parabola of the medial triangle, and lies on the nine-point circle and the orthic inconic. Its perspector is the intersection of the orthic axis and the Lemoine axis.	${\displaystyle {\begin{aligned}&{\frac {a(\sin 2B-\sin 2C)}{x}}+{\frac {b(\sin 2C-\sin 2A)}{y}}\\[2pt]&+{\frac {c(\sin 2A-\sin 2B)}{z}}=0\end{aligned}}}$	Jerabek hyperbola of △ABC
3	Feuerbach hyperbola [10]	Rectangular hyperbola passing through the vertices, the orthocenter and the incenter of △ABC. Isogonal conjugate of ${\displaystyle OI}$, the line joining the circumcenter and the incenter. Its center, the orthopole of ${\displaystyle OI}$, is the Feuerbach point, and lies on the incircle, the nine-point circle and the Mandart inellipse. Its perspector is the intersection of the orthic axis, the antiorthic axis and the Gergonne line.	${\displaystyle {\frac {\cos B-\cos C}{x}}+{\frac {\cos C-\cos A}{y}}+{\frac {\cos A-\cos B}{z}}=0}$	Feuerbach Hyperbola of △ABC
4	Dual of the Yff parabola [16] [12] [17] [10]	Hyperbola passing through the vertices, the centroid and the Gergonne point of △ABC. Isotomic conjugate of the Nagel line. Its center is the perspector of the Yff parabola of the medial triangle, and lies on the Steiner inellipse. Its perspector is the intersection of the Gergonne line and the line at infinity.	${\displaystyle {\frac {bc(b-c)}{x}}+{\frac {ca(c-a)}{y}}+{\frac {ab(a-b)}{z}}=0}$

Note: The pedal circle of any point on a rectangular circumhyperbola passes through the hyperbola's center. Since all such hyperbolas pass through the orthocenter, their centers all lie on the nine-point circle. ^[8]

Triangle parabolas

Some well known triangle parabolas

No.	Name	Definition	Equation	Figure
1	Artzt parabolas [18] [19] [20]	A parabola (the A-Artzt parabola) tangent at B, C to the sides AB, AC, and two other similar parabolas. The directrix of the A-Artzt parabola is the perpendicular to the median through A at its intersection, beside the midpoint of BC, with the nine-point circle. The focus of the A-Artzt parabola is the intersection of the symmedian through A, beside the symmedian point, with the Brocard circle.	${\displaystyle {\begin{aligned}{\frac {x^{2}}{a^{2}}}-{\frac {4yz}{bc}}&=0\\[2pt]{\frac {y^{2}}{b^{2}}}-{\frac {4xz}{ca}}&=0\\[2pt]{\frac {z^{2}}{c^{2}}}-{\frac {4xy}{ab}}&=0\end{aligned}}}$	Artzt parabolas of △ABC
2	Kiepert parabola [21] [10]	Let three similar isosceles triangles △A'BC, △AB'C, △ABC' be constructed on the sides of △ABC. Then the envelope of the perspectrix of the triangles △ABC and △A'B'C' is Kiepert's parabola. The Kiepert parabola has the Euler line as its directrix. Its focus is the trilinear pole of the Brocard axis, the orthocorrespondent of the center of the Kiepert hyperbola, the center of the Jerabek hyperbola of the anticomplementary triangle and, if △ABC is acute, the Feuerbach point of the tangential triangle. Its perspector is the Steiner point, which lies on the circumcircle and the Steiner ellipse.	${\displaystyle {\begin{aligned}&f^{2}x^{2}+g^{2}y^{2}+h^{2}z^{2}-\\[2pt]&2fgxy-2ghyz-2hfxz=0,\\[8pt]&{\text{where }}f=b^{2}-c^{2},\\&g=c^{2}-a^{2},\ h=a^{2}-b^{2}.\end{aligned}}}$	Kiepert parabola of △ABC. The figure also shows a member (line LMN) of the family of lines whose envelope is the Kiepert parabola.
3	Yff parabola [16] [10]	Parabola tangent to the sides of △ABC whose directrix is the Brocard axis of the excentral triangle and whose focus is the center of the Kiepert hyperbola of the excentral triangle. Its perspector is the trilinear pole of the Nagel line, and lies on the Steiner ellipse.	${\displaystyle {\begin{aligned}&f^{2}x^{2}+g^{2}y^{2}+h^{2}z^{2}-\\[2pt]&2fgxy-2ghyz-2hfxz=0,\\[8pt]&{\text{where }}f=a^{2}(b-c)^{2},\\&g=b^{2}(c-a)^{2},\ h=c^{2}(a-b)^{2}.\end{aligned}}}$

Families of triangle conics

Hofstadter ellipses

Family of Hofstadter conics of △ABC

An Hofstadter ellipse ^[22] is a member of a one-parameter family of ellipses in the plane of △ABC defined by the following equation in trilinear coordinates: $${\displaystyle x^{2}+y^{2}+z^{2}+yz\left[D(t)+{\frac {1}{D(t)}}\right]+zx\left[E(t)+{\frac {1}{E(t)}}\right]+xy\left[F(t)+{\frac {1}{F(t)}}\right]=0}$$ where t is a parameter and $${\displaystyle {\begin{aligned}D(t)&=\cos A-\sin A\cot tA\\E(t)&=\cos B-\sin B\cot tB\\F(t)&=\sin C-\cos C\cot tC\end{aligned}}}$$ The ellipses corresponding to t and 1 −t are identical. When t = 1/2 we have the inellipse $${\displaystyle x^{2}+y^{2}+z^{2}-2yz-2zx-2xy=0}$$ and when t → 0 we have the circumellipse $${\displaystyle {\frac {a}{Ax}}+{\frac {b}{By}}+{\frac {c}{Cz}}=0.}$$

Conics of Thomson and Darboux

The family of Thomson conics consists of those conics inscribed in the reference triangle △ABC having the property that the normals at the points of contact with the sidelines are concurrent. The family of Darboux conics contains as members those circumscribed conics of the reference △ABC such that the normals at the vertices of △ABC are concurrent. In both cases the points of concurrency lie on the Darboux cubic. ^{[23] [24]}

Conic associated with parallel intercepts

Conics associated with parallel intercepts

Given an arbitrary point in the plane of the reference triangle △ABC, if lines are drawn through P parallel to the sidelines BC, CA, AB intersecting the other sides at X_b, X_c, Y_c, Y_a, Z_a, Z_b then these six points of intersection lie on a conic. If P is chosen as the symmedian point, the resulting conic is a circle called the first Lemoine circle. If the trilinear coordinates of P are u : v : w the equation of the six-point conic is ^[8] $${\displaystyle -(au+bv+cw)^{2}(uyz+vzx+wxy)+(ax+by+cz)(vw(bv+cw)x+wu(cw+au)y+uv(au+bv)z)=0}$$

Yff conics

Yff Conics

The members of the one-parameter family of conics defined by the equation $${\displaystyle x^{2}+y^{2}+z^{2}-2\lambda (yz+zx+xy)=0,}$$ where ${\displaystyle \lambda }$ is a parameter, are the Yff conics associated with the reference triangle △ABC. ^[25] A member of the family is associated with every point P(u : v : w) in the plane by setting $${\displaystyle \lambda ={\frac {u^{2}+v^{2}+w^{2}}{2(vw+wu+uv)}}.}$$ The Yff conic is a parabola if $${\displaystyle \lambda ={\frac {a^{2}+b^{2}+c^{2}}{a^{2}+b^{2}+c^{2}-2(bc+ca+ab)}}=\lambda _{0}}$$ (say). It is an ellipse if ${\displaystyle \lambda <\lambda _{0}}$ and ${\displaystyle \lambda _{0}>{\frac {1}{2}}}$ and it is a hyperbola if ${\displaystyle \lambda _{0}<\lambda <-1}$. For ${\displaystyle -1<\lambda <{\frac {1}{2}}}$, the conics are imaginary.

See also

• Triangle center
• Central line
• Triangle cubic
• Modern triangle geometry

References

1. Paris Pamfilos (2021). "Equilaterals Inscribed in Conics". International Journal of Geometry. 10 (1): 5–24.
2. Christopher J Bradley. "Four Triangle Conics". Personal Home Pages. University of BATH. Retrieved 11 November 2021.
3. Gotthard Weise (2012). "Generalization and Extension of the Wallace Theorem". Forum Geometricorum. 12: 1–11. Retrieved 12 November 2021.
4. Zlatan Magajna. "OK Geometry Plus". OK Geometry Plus. Retrieved 12 November 2021.
5. "Geometrikon". Paris Pamfilos home page on Geometry, Philosophy and Programming. Paris Palmfilos. Retrieved 11 November 2021.
6. "1. Triangle conics". Paris Pamfilos home page on Geometry, Philosophy and Programming. Paris Palfilos. Retrieved 11 November 2021.
7. Bernard Gibert. "Catalogue of Triangle Cubics". Cubics in Triangle Plane. Bernard Gibert. Retrieved 12 November 2021.
8. Paul Yiu (Summer 2001). Introduction to the Geometry of the Triangle (PDF). pp. 127, 133, 141. Retrieved 11 October 2025.
9. "Triangle conics". Paris Pamfilos home page on Geometry, Philosophy and Programming. Paris Palfilos. Retrieved 11 October 2025.
10. Kimberling, Clark. "Encyclopedia of Triangle Centers" . Retrieved 29 June 2025. See X(11) = Feuerbach point, X(101) = Ψ(incenter, symmedian point), X(110) = Focus of Kiepert parabola, X(115) = Center of Kiepert hyperbola, X(125) = Center of Jerabek hyperbola, X(190) = Yff parabolic point, X(514) = Isogonal conjugate of X(101), X(523) = Isogonal conjugate of X(110), X(647) = Crossdifference of X(2) and X(3), and X(650) = Crossdifference of X(1) and X(3).
11. Weisstein, Eric W. "Perspector". MathWorld--A Wolfram Web Resource. Wolfram Research. Retrieved 23 June 2025.
12. Stothers, Wilson. "circumconics and inconics". www.maths.gla.ac.uk. Retrieved 23 June 2025.
13. "Projectivities play related to a triangle". Paris Pamfilos home page on Geometry, Philosophy and Programming. Paris Palfilos. Retrieved 23 June 2025.
14. Nelle May Cook (1929). A Triangle and its Circles (PDF). Kansas State Agricultural College. Retrieved 12 November 2021.
15. Weisstein, Eric W. "Tucker Circles". MathWorld--A Wolfram Web Resource. Wolfram Research. Retrieved 11 October 2025.
16. Weisstein, Eric W. "Yff Parabola". MathWorld--A Wolfram Web Resource. Wolfram Research. Retrieved 20 June 2025.
17. Kimberling, Clark. "Encyclopedia of Triangle Centers" . Retrieved 1 July 2025. See X(1086) = Center of hyperbola {{A,B,C,X(2),X(7)|}.
18. Nikolaos Dergiades (2010). "Conics Tangent at the Vertices to Two Sides of a Triangle". Forum Geometricorum. 10: 41–53.
19. Sharp, John (2 November 2015). "Artzt parabolas of a triangle". The Mathematical Gazette. 99 (546). Cambridge University Press: 454, 458. doi:10.1017/mag.2015.81 . Retrieved 11 October 2025.
20. "Symmedian" (PDF). Paris Pamfilos home page on Geometry, Philosophy and Programming. Paris Palfilos. 15 May 2021. Retrieved 24 June 2025.
21. R H Eddy and R Fritsch (June 1994). "The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle". Mathematics Magazine. 67 (3): 188–205. doi:10.1080/0025570X.1994.11996212.
22. Weisstein, Eric W. "Hofstadter Ellipse". MathWorld--A Wolfram Web Resource. Wolfram Research. Retrieved 25 November 2021.
23. Roscoe Woods (1932). "Some Conics with Names". Proceedings of the Iowa Academy of Science. 39 Volume 50 (Annual Issue).
24. "K004 : Darboux cubic". Catalogue of Cubic Curves. Bernard Gibert. Retrieved 26 November 2021.
25. Clark Kimberling (2008). "Yff Conics". Journal for Geometry and Graphics. 12 (1): 23–34.