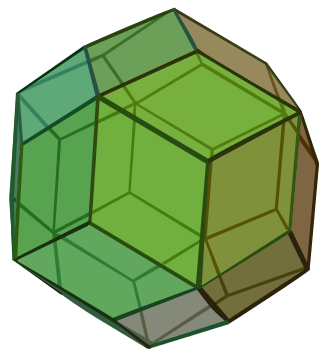
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.
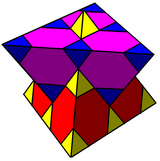
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.

In geometry, a trigonal trapezohedron is a rhombohedron in which, additionally, all six faces are congruent. Alternative names for the same shape are the trigonal deltohedron or isohedral rhombohedron. Some sources just call them rhombohedra.

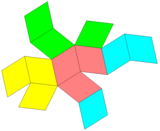
In geometry, the trapezo-rhombic dodecahedron or rhombo-trapezoidal dodecahedron is a convex dodecahedron with 6 rhombic and 6 trapezoidal faces. It has D3h symmetry. A concave form can be constructed with an identical net, seen as excavating trigonal trapezohedra from the top and bottom. It is also called the trapezoidal dodecahedron.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

The rhombic dodecahedral honeycomb is a space-filling tessellation in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which has the densest possible packing of equal spheres in ordinary space.

The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.

The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an oblate tetrahedrille or shortened to obtetrahedrille.

In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex. It has Schläfli symbol of r{7,3}.

In geometry, the order-5 square tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {4,5}.

In geometry, the 3-7 kisrhombille tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 14 triangles meeting at each vertex.

The triakis truncated tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of triakis truncated tetrahedra. It was discovered in 1914.

In geometry, the tetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol r{6,4}.

In geometry, the trioctagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 octagonal tiling. There are two triangles and two octagons alternating on each vertex. It has Schläfli symbol of r{8,3}.

In geometry, the infinite-order triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,∞}. All vertices are ideal, located at "infinity" and seen on the boundary of the Poincaré hyperbolic disk projection.