Blowfish is a symmetric-key block cipher, designed in 1993 by Bruce Schneier and included in many cipher suites and encryption products. Blowfish provides a good encryption rate in software, and no effective cryptanalysis of it has been found to date for smaller files. It is recommended Blowfish should not be used to encrypt files larger than 4GB in size, Twofish should be used instead.

In cryptography, an HMAC is a specific type of message authentication code (MAC) involving a cryptographic hash function and a secret cryptographic key. As with any MAC, it may be used to simultaneously verify both the data integrity and authenticity of a message. An HMAC is a type of keyed hash function that can also be used in a key derivation scheme or a key stretching scheme.
The MD5 message-digest algorithm is a widely used hash function producing a 128-bit hash value. MD5 was designed by Ronald Rivest in 1991 to replace an earlier hash function MD4, and was specified in 1992 as RFC 1321.
Adler-32 is a checksum algorithm written by Mark Adler in 1995, modifying Fletcher's checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32.
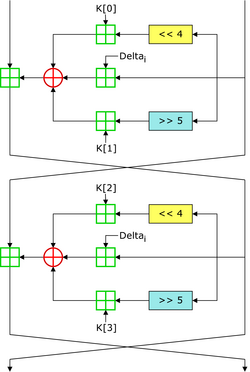
In cryptography, the Tiny Encryption Algorithm (TEA) is a block cipher notable for its simplicity of description and implementation, typically a few lines of code. It was designed by David Wheeler and Roger Needham of the Cambridge Computer Laboratory; it was first presented at the Fast Software Encryption workshop in Leuven in 1994, and first published in the proceedings of that workshop.
The Fletcher checksum is an algorithm for computing a position-dependent checksum devised by John G. Fletcher (1934–2012) at Lawrence Livermore Labs in the late 1970s. The objective of the Fletcher checksum was to provide error-detection properties approaching those of a cyclic redundancy check but with the lower computational effort associated with summation techniques.
In computer architecture, 128-bit integers, memory addresses, or other data units are those that are 128 bits wide. Also, 128-bit central processing unit (CPU) and arithmetic logic unit (ALU) architectures are those that are based on registers, address buses, or data buses of that size.
Poly1305 is a universal hash family designed by Daniel J. Bernstein in 2002 for use in cryptography.
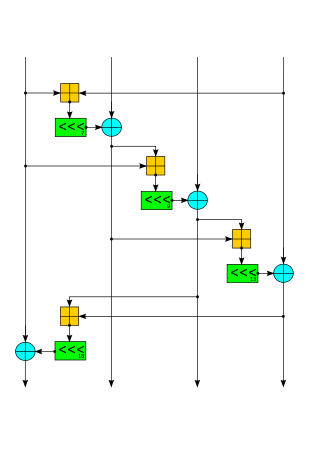
Salsa20 and the closely related ChaCha are stream ciphers developed by Daniel J. Bernstein. Salsa20, the original cipher, was designed in 2005, then later submitted to the eSTREAM European Union cryptographic validation process by Bernstein. ChaCha is a modification of Salsa20 published in 2008. It uses a new round function that increases diffusion and increases performance on some architectures.
The GOST hash function, defined in the standards GOST R 34.11-94 and GOST 34.311-95 is a 256-bit cryptographic hash function. It was initially defined in the Russian national standard GOST R 34.11-94 Information Technology – Cryptographic Information Security – Hash Function. The equivalent standard used by other member-states of the CIS is GOST 34.311-95.
In mathematics and computing, universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property. This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary. Many universal families are known, and their evaluation is often very efficient. Universal hashing has numerous uses in computer science, for example in implementations of hash tables, randomized algorithms, and cryptography.
CubeHash is a cryptographic hash function submitted to the NIST hash function competition by Daniel J. Bernstein. CubeHash has a 128 byte state, uses wide pipe construction, and is ARX based. Message blocks are XORed into the initial bits of a 128-byte state, which then goes through an r-round bijective transformation between blocks. The initial NIST proposal ("Cubehash8/1") required about 200 cycles per byte. After clarifications from NIST, the author changed the proposal to Cubehash16/32, which "is approximately 16 times faster than CubeHash8/1, easily catching up to both SHA-256 and SHA-512 on the reference platform" while still maintaining a "comfortable security margin".
bcrypt is a password-hashing function designed by Niels Provos and David Mazières, based on the Blowfish cipher and presented at USENIX in 1999. Besides incorporating a salt to protect against rainbow table attacks, bcrypt is an adaptive function: over time, the iteration count can be increased to make it slower, so it remains resistant to brute-force search attacks even with increasing computation power.
The Jenkins hash functions are a family of non-cryptographic hash functions for multi-byte keys designed by Bob Jenkins. The first one was formally published in 1997.
MurmurHash is a non-cryptographic hash function suitable for general hash-based lookup. It was created by Austin Appleby in 2008 and, as of 8 January 2016, is hosted on GitHub along with its test suite named SMHasher. It also exists in a number of variants, all of which have been released into the public domain. The name comes from two basic operations, multiply (MU) and rotate (R), used in its inner loop.
VMAC is a block cipher-based message authentication code (MAC) algorithm using a universal hash proposed by Ted Krovetz and Wei Dai in April 2007. The algorithm was designed for high performance backed by a formal analysis.
BLAKE is a cryptographic hash function based on Daniel J. Bernstein's ChaCha stream cipher, but a permuted copy of the input block, XORed with round constants, is added before each ChaCha round. Like SHA-2, there are two variants differing in the word size. ChaCha operates on a 4×4 array of words. BLAKE repeatedly combines an 8-word hash value with 16 message words, truncating the ChaCha result to obtain the next hash value. BLAKE-256 and BLAKE-224 use 32-bit words and produce digest sizes of 256 bits and 224 bits, respectively, while BLAKE-512 and BLAKE-384 use 64-bit words and produce digest sizes of 512 bits and 384 bits, respectively.
Badger is a message authentication code (MAC) based on the idea of universal hashing and was developed by Boesgaard, Scavenius, Pedersen, Christensen, and Zenner. It is constructed by strengthening the ∆-universal hash family MMH using an ϵ-almost strongly universal (ASU) hash function family after the application of ENH, where the value of ϵ is . Since Badger is a MAC function based on the universal hash function approach, the conditions needed for the security of Badger are the same as those for other universal hash functions such as UMAC.
Argon2 is a key derivation function that was selected as the winner of the 2015 Password Hashing Competition. It was designed by Alex Biryukov, Daniel Dinu, and Dmitry Khovratovich from the University of Luxembourg. The reference implementation of Argon2 is released under a Creative Commons CC0 license or the Apache License 2.0, and provides three related versions:
LSH is a cryptographic hash function designed in 2014 by South Korea to provide integrity in general-purpose software environments such as PCs and smart devices. LSH is one of the cryptographic algorithms approved by the Korean Cryptographic Module Validation Program (KCMVP). And it is the national standard of South Korea.











