
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard.
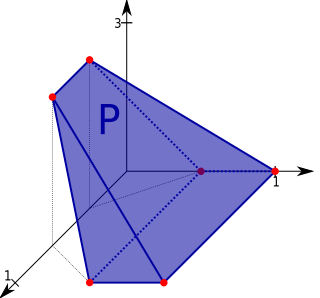
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices; thus, it can be described as "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.

In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cube graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n – 1n edges, and is a regular graph with n edges touching each vertex.
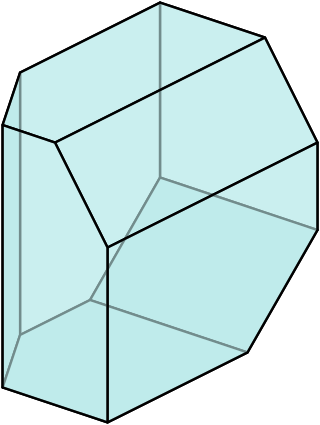
In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges (also d facets). The vertex figure of a simple d-polytope is a (d – 1)-simplex.
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

In geometry, Keller's conjecture is the conjecture that in any tiling of n-dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire (n − 1)-dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration.
In the study of algorithms, an LP-type problem is an optimization problem that shares certain properties with low-dimensional linear programs and that may be solved by similar algorithms. LP-type problems include many important optimization problems that are not themselves linear programs, such as the problem of finding the smallest circle containing a given set of planar points. They may be solved by a combination of randomized algorithms in an amount of time that is linear in the number of elements defining the problem, and subexponential in the dimension of the problem.

In graph theory, an acyclic orientation of an undirected graph is an assignment of a direction to each edge that does not form any directed cycle and therefore makes it into a directed acyclic graph. Every graph has an acyclic orientation.
In geometry, a Hanner polytope is a convex polytope constructed recursively by Cartesian product and polar dual operations. Hanner polytopes are named after Olof Hanner, who introduced them in 1956.
In geometry, Kalai's 3d conjecture is a conjecture on the polyhedral combinatorics of centrally symmetric polytopes, made by Gil Kalai in 1989. It states that every d-dimensional centrally symmetric polytope has at least 3d nonempty faces.
In graph theory, a bipolar orientation or st-orientation of an undirected graph is an assignment of a direction to each edge that causes the graph to become a directed acyclic graph with a single source s and a single sink t, and an st-numbering of the graph is a topological ordering of the resulting directed acyclic graph.

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.
Reverse-search algorithms are a class of algorithms for generating all objects of a given size, from certain classes of combinatorial objects. In many cases, these methods allow the objects to be generated in polynomial time per object, using only enough memory to store a constant number of objects. They work by organizing the objects to be generated into a spanning tree of their state space, and then performing a depth-first search of this tree.












